Riemannen integral

Riemannen integrala edo integral mugatua, Bernhard Riemannek sorturikoa, tarte baten gainean funtzio baten integralaren lehengo definizio zehatza izan zen.

Izan bitez ${\displaystyle f(x)}$, ${\displaystyle [a,b]}$ tartean jarraitua eta positiboa den funtzio bat, eta ${\displaystyle S=\{(x,y)|a<x<b{\text{ eta }}0<y<f(x)\}}$ planoko barruti itxia ${\displaystyle f(x)}$ funtzioaren azpian (ikusi irudia). Orduan, Riemannek ${\displaystyle f(x)}$ funtzioaren integrala ${\displaystyle [a,b]}$ tartean modu arrazan definitzen du honela:

${\displaystyle \int _{a}^{b}f(x)\,dx=A(f,a,b)}$ , non ${\displaystyle A(f,a,b)}$ ${\displaystyle S}$-ren azalera den.

${\displaystyle S}$ barrutiaren azalera neurtu nahi dugu, neurgarria bada.

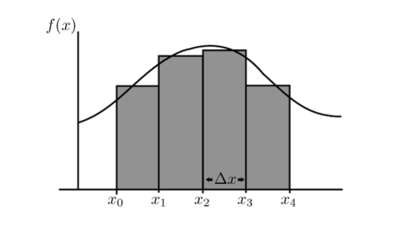
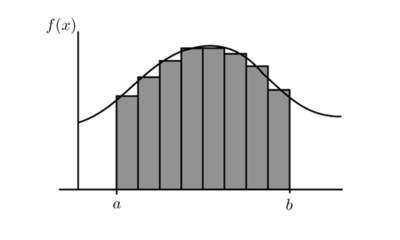
Azalera horren balioa kalkulatzeko elkarren ondoan jarritako laukizuzenen bidez hurbilduko da barrutia, irudian adierazten den moduan.

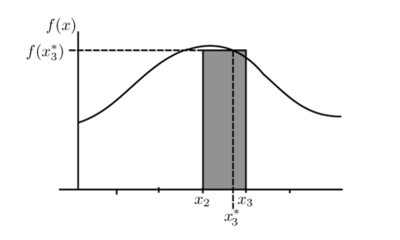
Laukizuzen bakoitzaren azalera, funtzioaren balioa oinarriaren edozein puntutan, bider oinarriaren luzera da. Zenbat eta laukizuzen gehiago hartu, orduan eta txikiagoa izango da laukizuzen horien oinarria, baina orduan eta hurbilago izango dira batura horiek ${\displaystyle A(f,a,b)}$ baliotik.

Honela adierazten da:

${\displaystyle \int _{a}^{b}f(x)dx=}$ ${\displaystyle \lim _{n\to \infty }\sum _{i=0}^{n-1}f(x_{i}^{*})\Delta x_{i-1}}$

Ikus, gainera

Riemannen batura

Kanpo estekak

• Datuak: Q697181
• Multimedia: Riemann integral / Q697181