Turunan

Kalkulus
Teorema dasar Limit fungsi Kontinuitas Teorema nilai purata Teorema Rolle
Diferensial Definisi Turunan (perumuman) Tabel turunan Diferensial infinitesimal fungsi total Konsep Notasi untuk pendiferensialan Turunan kedua Turunan ketiga Perubahan variabel Pendiferensialan implisit Laju yang berkaitan Teorema Taylor Kaidah dan identitas Kaidah penjumlahan dalam pendiferensialan Perkalian Rantai Pangkat Pembagian Rumus Faà di Bruno
Integral Definisi Antiderivatif Integral (takwajar) Integral Riemann Integrasi Lebesgue Integrasi kontur Tabel integral Integrasi secara parsial cakram kulit tabung substitusi (trigonometri) pecahan parsial Urutan Rumus reduksi
Deret geometri (aritmetika-geometrik) harmonik selang-seling pangkat binomial Taylor Uji kekonvergenan uji suku rasio akar integral perbandingan langsung perbandingan limit deret selang-seling kondensasi Cauchy Dirichlet Abel
Vektor Gradien Divergence Keikalan Laplace berarah identitas Teorema Kedivergenan Gradien Green Stokes
Multivariabel Formalisme matriks tensor eksterior geometrik Definisi Turunan parsial Integral lipat Integral garis Permukaan integral integral volume Jacobi Hesse
Khusus fraksional Malliavin stokastik variasi
l b s

Dalam matematika, turunan atau derivatif dari sebuah fungsi adalah cara mengukur sensitivitas perubahan nilai fungsi terhadap perubahan pada nilai variabelnya. Sebagai contoh, turunan dari posisi sebuah benda bergerak terhadap waktu mengukur kecepatan benda bergerak ketika waktu berjalan. Turunan adalah alat penting dalam kalkulus.

Turunan sebuah fungsi satu variabel di suatu titik, jika itu ada, adalah kemiringan dari garis singgung dari grafik fungsi di titik tersebut. Garis singgung adalah hampiran (aproksimasi) linear terbaik dari fungsi di sekitar titik tersebut. Konsep turunan dapat diperumum untuk fungsi multivariabel. Dalam perumuman ini, turunan dianggap sebagai transformasi linear, dengan translasi yang sesuai, menghasilkan hampiran linear dari grafik fungsi multivariabel tersebut. Matriks Jacobi adalah matriks yang merepresentasikan transformasi linear terhadap suatu basis yang ditentukan. Matriks ini dapat ditentukan dengan turunan parsial dari variabel-variabel independen. Pada fungsi multivariabel bernilai real, matriks Jacobi tereduksi menjadi vektor gradien.

Proses menemukan turunan disebut diferensiasi. Kebalikan proses ini disebut dengan antiturunan. Teorema fundamental kalkulus menyatakan hubungan diferensiasi dengan integrasi. Turunan dan integral adalah dua operasi dasar dalam kalkulus satu-variabel.

Konsep turunan fungsi yang universal banyak digunakan dalam berbagai cabang matematika maupun bidang ilmu yang lain. Dalam bidang ekonomi, turunan digunakan untuk menghitung biaya marginal, total penerimaan, dan biaya produksi. Bidang biologi menggunakan turunan untuk menghitung laju pertumbuhan mikroorganisme, dalam bidang fisika untuk menghitung kepadatan kawat, dalam bidang kimia untuk menghitung laju pemisahan, dalam bidang geografi untuk menghitung laju pertumbuhan penduduk, dan masih banyak lagi.

Pendahuluan

Secara informal, turunan dari sebuah fungsi y = f(x) dengan variabel x adalah ukuran dari rasio perubahan nilai y terhadap perubahan nilai variabel x. Jika x dan y adalah bilangan real, dan jika grafik fungsi f diplot terhadap x, besar turunan dari fungsi ini pada sembarang titik menandakan kemiringan dari grafik fungsi pada titik tersebut.

Kasus sederhana dari fungsi f(x) adalah fungsi linear yang memiliki persamaan y = f(x) = mx + b, dengan bilangan real m dan b. Kemiringan dari fungsi ini, m, dinyatakan dengan

${\displaystyle m={\frac {{\text{perubahan nilai }}y}{{\text{perubahan nilai }}x}}={\frac {\Delta y}{\Delta x}},}$

dengan simbol Δ (Delta) adalah singkatan untuk "perubahan nilai", dan simbol ${\displaystyle \Delta x}$ dan ${\displaystyle \Delta y}$ masing-masing menyatakan besar perubahan yang terjadi. Sebagai contoh,

Persamaan di atas berlaku, karenadan menghasilkan persamaan ${\displaystyle \Delta y=m\Delta x}$ yang memberikan persamaan kemiringan dari suatu garis.

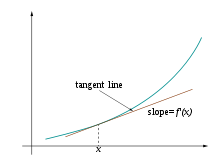
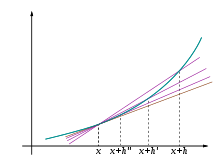
Jika fungsi f tidak linear (maksudnya grafik fungsi bukan berupa garis lurus), maka perubahan nilai y dibagi dengan perubahan nilai x dapat berubah-ubah tergantung nilai perubahan nilai x yang dipilih. Turunan adalah metode untuk menentukan nilai unik dari perbandingan perubahan nilai tersebut, yang tidak tergantung besar perubahan ${\displaystyle (\Delta x),}$ melainkan titik x yang dipilih. Metode menentukan turunan dapat diilustrasikan lewat Gambar 1 sampai Gambar 3, yang menggambarkan nilai limit dari perbandingan Δy / Δx dengan besar Δx menuju 0.

Asal-usul definisi

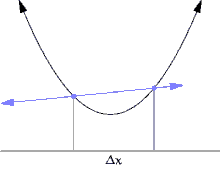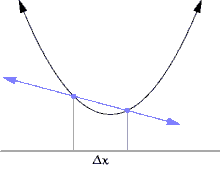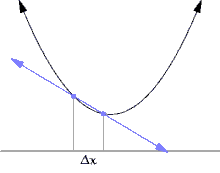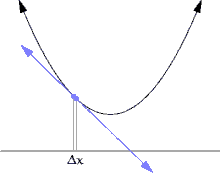
Salah satu cara umum untuk menyatakan cara diferensiasi yang intuitif ke dalam definisi yang matematis adalah dengan mendefinisikan turunan sebagai limit dari perbandingan dua bilangan real.^[1] Pendekatan ini dapat dijabarkan sebagai berikut.

Misalkan f adalah fungsi bernilai real yang terdefinisi pada suatu lingkungan buka dari suatu bilangan real a. Dalam geometri, garis singgung dari grafik fungsi f di a adalah suatu garis unik yang melalui titik (a, f(a)) dan tidak memotong fungsi f di sekitar titik (a, f(a)). Turunan dari y terhadap x di a secara geometris adalah besar kemiringan dari garis singgung grafik f di (a, f(a)). Besar kemiringan garis singgung akan sangat mirip dengan besar kemiringan garis yang melalui titik (a, f(a)) dan sebuah titik lain di grafik yang dekat dengannya, sebagai contoh (a + h, f(a + h)). Garis yang didefinisikan ini disebut dengan garis sekan. Nilai h yang dekat dengan nol akan memberikan hampiran (dugaan, aproksimasi) yang baik mengenai besar kemiringan garis singgung; dan secara umum, nilai (mutlak) h yang semakin kecil akan memberikan hampiran yang lebih baik. Besar kemiringan m dari garis sekan adalah perbedaan nilai y antara dua titik tersebut, dibagi dengan perbedaan nilai x pada dua titik yang sama, dengan kata lain

Limit digunakan untuk mengubah nilai hampiran ke nilai yang pasti (exact). Jika nilai dari limit ketika h menuju nol ada, maka nilai ini menyatakan besar kemiringan dari garis singgung fungsi di titik (a, f(a)). Limit ini didefinisikan sebagai turunan dari fungsi f di a:

Jika nilai limit ada, f dikatakan terdiferensialkan di a. Notasi ${\displaystyle f'(a)}$ adalah salah satu notasi umum untuk turunan. Definisi turunan ini mengandung hubungan yang intuitif bahwa suatu fungsi terdiferensialkan f bersifat menaik jika dan hanya jika turunannya bernilai positif, dan menurun jika dan hanya jika turunannya bernilai negatif. Fakta ini sering digunakan dalam analisis mengenai perilaku fungsi, contohnya dalam menentukan titik ekstrem fungsi.

Selain itu, turunan juga memenuhi sifat

yang menghasilkan interpretasi yang intuitif (lihat Gambar 1) bahwa garis singgung fungsi f di a memberikan hampiran linear terbaik

untuk nilai fungsi f di sekitar a (yakni, untuk nilai h yang kecil). Interpretasi ini adalah konsep termudah yang dapat diperumum ke kasus-kasus lainnya.

Metode subtitusi h dengan nol pada perbandingan beda tidak dapat dilakukan karena menghasilkan pembagian oleh nol. Hal ini menyebabkan besar kemiringan dari garis singgung tidak dapat ditemukan secara langsung lewat subtitusi. Besar kemiringan dapat ditentukan mendefinisikan Q(h) menjadi perbandingan (quotinent) beda sebagai fungsi dari h:

${\displaystyle Q(h)}$ secara geometris menyatakan kemiringan dari garis sekan yang melalui ${\displaystyle (a,\,f(a))}$ dan ${\displaystyle (a+h,\,f(a+h))}$. Jika f adalah fungsi kontinu, secara informal mengartikan grafik fungsinya berupa kurva tak putus dan tidak mengandung celah, maka fungsi Q kontinu selain di ${\displaystyle h=0}$. Jika limit ${\displaystyle \lim _{h\to 0}Q(h)}$ ada, maka ada cara lain memilih nilai untuk Q(0) yang membuat Q menjadi fungsi kontinu, membuat fungsi f terdiferensialkan di a, dan besar turunannya di a sama dengan Q(0). Pada praktiknya, keberadaan Q(h) yang kontinu di ${\displaystyle h=0}$ ditunjukkan dengan mengubah ekspresi pada pembilang agar dapat "mencoret" semua suku h pada penyebut. Manipulasi seperti itu memungkinkan nilai limit dari Q untuk nilai h yang kecil terlihat jelas, walaupun Q masih tidak terdefinisi di ${\displaystyle h=0}$. Proses manipulasi ini dapat sangat panjang dan melelahkan untuk fungsi yang rumit, dan banyak jalan pintas digunakan untuk menyederhanakan proses.

Contoh perhitungan

Fungsi kuadrat memiliki persamaan f(x) = x² dan diferensialkan di x = 3, dengan nilai turunan fungsi di titik tersebut adalah 6. Hasil ini didapatkan dari menghitung limit dengan h menuju nol, dari persamaan beda f(3):

Ekspresi terakhir menunjukkan persamaan beda sama dengan ekspresi 6 + h saat ${\displaystyle h\neq 0}$ dan tidak terdefinisi saat h = 0, karena definisi dari persamaan beda. Tetapi, definisi dari limit menyatakan persamaan beda tidak harus terdefinisi saat h = 0. Nilai limit adalah hasil dari membuat variabel h menuju nol, mengartikan ekspresi 6 + h saat nilai h menuju sekecil mungkin akan menjadi:Mengartikan kemiringan dari grafik fungsi kuadrat di titik (3, 9) adalah 6, dan turunannya di x = 3 adalah ${\displaystyle f'(3)=6}$. Secara umum, perhitungan yang sama dapat digunakan untuk menunjukkan bahwa turunan fungsi kuadrat di x = a adalah ${\displaystyle f'(a)=2a}$:

${\displaystyle {\begin{aligned}f'(a)&=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}=\lim _{h\to 0}{\frac {(a+h)^{2}-a^{2}}{h}}\\[0.3em]&=\lim _{h\to 0}{\frac {a^{2}+2ah+h^{2}-a^{2}}{h}}=\lim _{h\to 0}{\frac {2ah+h^{2}}{h}}\\[0.3em]&=\lim _{h\to 0}{(2a+h)}=2a\end{aligned}}}$

Sejarah

Kalkulus, atau dikenal dalam sejarah lebih awalnya, kalkulus infinitesimal, merupakan cabang matematika yang berfokus pada konsep limit, fungsi, turunan, integral, dan deret takhingga. Isaac Newton dan Gottfried Leibniz menemukan kalkulus secara terpisah pada pertengahan abad ke-17. Namun dalam pertikaian yang pahit, Leibniz dituduh bahwa ia mencuri karya Newton dan sebaliknya. Pertikaian ini berlanjut hingga kematian mereka berdua.

Definisi

Sebuah fungsi dengan variabel real, ${\displaystyle y=f(x)}$, dikatakan terdiferensialkan atau dapat diturunkan pada suatu titik ${\displaystyle a}$ di domainnya, jika domain fungsi tersebut mengandung suatu interval buka ${\displaystyle I}$ yang beranggotakan ${\displaystyle a}$, dan nilai limit

ada. Hal ini mengartikan bahwa, untuk setiap bilangan real positif ${\displaystyle \varepsilon }$ (bahkan jika nilainya sangat kecil), akan ada suatu bilangan real positif ${\displaystyle \delta }$ sedemikian sehingga, untuk semua h yang memenuhi ${\displaystyle |h|<\delta }$ dan ${\displaystyle h\neq 0}$, menyebabkan nilai ${\displaystyle f(a+h)}$ terdefinisi dandengan bar vertikal menyatakan nilai mutlak (lihat definisi epsilon-delta dari limit).

Jika fungsi ${\displaystyle f}$ terdiferensialkan di ${\displaystyle a}$, dengan kata lain jika nilai limit ${\displaystyle L}$ ada, maka nilai limit ini disebut turunan dari ${\displaystyle f}$ di ${\displaystyle a}$, dan dinyatakan dengan ${\displaystyle f'(a)}$ atau ${\textstyle {\frac {df}{dx}}(a)}$ (dibaca "turunan dari ${\displaystyle f}$ terhadap ${\displaystyle x}$ di ${\displaystyle a}$" atau "dy per dx di ${\displaystyle a}$").

Kekontinuan dan keterdiferensialan

Fungsi ${\displaystyle f}$ yang terdiferensialkan di suatu titik ${\displaystyle a}$, juga akan bersifat kontinu di titik tersebut. Sebagai contoh dari sifat ini, misalkan f adalah fungsi tangga yang menghasilkan nilai 1 untuk semua x kurang dari nilai a, dan menghasilkan nilai yang berbeda, misalnya 10, untuk semua nilai x yang lebih besar atau sama dengan a. Fungsi f tidak dapat memiliki turunan di titik a. Untuk nilai h yang negatif, titik a + h akan terletak di sisi rendah dari fungsi tangga, menjadikan garis sekan dari a ke a + h akan sangat curam; dan semakin curam saat h menuju nol. Sedangkan nilai h yang positif, maka a + h terletak pada sisi tinggi dari fungsi tangga, sehingga garis sekan dari a ke a + h tidak memiliki kemiringan (datar). Alhasil garis-garis sekan tidak menuju besar kemiringan yang sama, mengakibatkan nilai limit dari persamaan beda tidak ada.

Tetapi, bahkan jika fungsi kontinu di suatu titik, fungsi tersebut mungkin tidak terdiferensialkan di sana. Sebagai contoh, fungsi nilai mutlak f(x) = |x| bersifat kontinu di x = 0, namun tidak terdiferensialkan di titik itu. Jika h positif, maka kemiringan dari garis sekan dari 0 ke h bernilai 1, sedangkan jika h negatif, maka kemiringan garis sekan dari 0 ke h bernilai -1. Bahkan fungsi mulus tidak dapat diturunkan di titik yang garis singgungnya merupakan garis vertikal: Sebagai contoh, fungsi f(x) = x^1/3 tidak terdiferensialkan di x = 0.

Secara singkat, fungsi yang terdiferensialkan adalah fungsi yang kontinu, tetapi ada fungsi kontinu yang tidak dapat didiferensialkan.

Sebagian besar fungsi pada praktiknya memiliki turunan di semua titik atau hampir semua titik. Pada awal sejarah kalkulus, banyak matematikawan mengasumsikan fungsi kontinu dapat diturunkan di banyak titik. Pada kondisi yang standar, hal ini berlaku karena kebanyakan fungsi adalah fungsi monoton atau fungsi Lipschitz. Tetapi pada tahun 1872, Weierstrass menemukan contoh pertama dari fungsi yang kontinu dimanapun namun tidak terdiferensialkan dimanapun. Contoh tersebut sekarang dikenal sebagai fungsi Weierstrass.

Turunan sebagai sebuah fungsi

Misalkan f adalah fungsi yang memiliki turunan di setiap titik di domainnya. Seseorang dapat mendefinisikan sebuah fungsi yang memetakan setiap titik x ke nilai dari turunan f di x. Salah satu notasi untuk menulis fungsi ini adalah ${\displaystyle f'}$, dan disebut sebagai fungsi turunan atau turunan dari f. Terkadang f memiliki turunan pada sebagian besar, tapi tidak semua, titik di domainnya. Fungsi yang nilainya di a sama dengan ${\displaystyle f'(a)}$ kapanpun nilai ${\displaystyle f'(a)}$ terdefinisi, dan tidak terdefinisi di nilai-nilai yang lainnya, juga disebut turunan dari f. Fungsi ini memiliki domain yang lebih kecil daripada domain dari f.

Menggunakan ide tersebut, turunan dapat dianggap sebagai fungsi dari fungsi: Turunan adalah sebuah operator dengan domainnya adalah himpunan semua fungsi yang memiliki turunan di semua titik pada domain mereka, dan citra-nya (range) adalah himpunan berisi fungsi-fungsi. Jika operator ini dinyatakan dengan D, maka D(f) sama dengan fungsi ${\displaystyle f'}$. Selain itu, karena D(f) adalah sebuah fungsi, nilainya dapat dihitung di titik a. Dengan menggunakan definisi dari fungsi turunan, ${\displaystyle D(f)(a)=f'(a).}$

Sebagai contoh, pertimbangkan fungsi f(x) = 2x; f adalah fungsi satu variabel yang bernilai real, mengartikan fungsi ini menerima sebuah angka lalu menghasilkan sebuah angka:

${\displaystyle {\begin{aligned}1&{}\mapsto 2,\\2&{}\mapsto 4,\\3&{}\mapsto 6.\end{aligned}}}$

Operator D di sisi lain, tidak menerima maupun menghasilkan angka, melainkan fungsi:

${\displaystyle {\begin{aligned}D(x\mapsto 1)&=(x\mapsto 0),\\D(x\mapsto x)&=(x\mapsto 1),\\D\left(x\mapsto x^{2}\right)&=(x\mapsto 2\cdot x).\end{aligned}}}$

Karena D menghasilkan sebuah fungsi, hasil dari D dapat dievaluasi di suatu titik. Sebagai contoh, ketika D diterapkan pada fungsi kuadrat x ↦ x², D akan menghasilkan fungsi x ↦ 2x, yang dapat diberi nama f(x). Fungsi hasil ini selanjutnya dapat digunakan untuk menghitung f(1) = 2, f(2) = 4, dan seterusnya.

Notasi turunan

Beberapa notasi untuk menyatakan turunan dikembangkan pada awal perkembangan kalkulus, dan beberapa notasi tersebut masih digunakan saat ini.

Notasi Leibniz

Simbol ${\displaystyle dx}$, ${\displaystyle dy}$, dan ${\displaystyle {\tfrac {dy}{dx}}}$ diperkenalkan oleh Gottfried Wilhelm Leibniz pada tahun 1675.^[2] Notasi ini masih umum digunakan ketika persamaan ${\displaystyle y=f(x)}$ ingin dipandang sebagai hubungan antara variabel terikat dan variabel bebas. Turunan pertama dengan notasi ini ditulis sebagai

dan awalnya dianggap sebagai perbandingan dua besaran infinitesimal ("infinitely small", "yang tak hingga kecilnya"). Turunan tingkat tinggi, yakni turunan ke-n dari ${\displaystyle y=f(x)}$, dituliskan sebagaiNotasi tersebut merupakan 'singkatan' dari penerapan operator turunan secara berulang. Sebagai contoh, notasi turunan kedua^[3]

${\displaystyle {\frac {d^{2}y}{dx^{2}}}={\frac {d}{dx}}\left({\frac {dy}{dx}}\right).}$

Dengan menggunakan notasi Leibniz, turunan dari ${\displaystyle y}$ di titik ${\displaystyle x=a}$ dapat ditulis dalam dua cara berbeda:

${\displaystyle \left.{\frac {dy}{dx}}\right|_{x=a}={\frac {dy}{dx}}(a).}$

Notasi Leibniz memungkinkan penulisan variabel diferensiasi (sebagai penyebut), yang berperan dalam turunan parsial. Notasi ini juga dapat digunakan untuk menulis aturan rantai sebagai^{[Note 1]}

${\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}.}$

Selain itu, notasi Leibniz memperlihatkan hubungan variabel yang sesuai dengan analisis dimensi. Sebagai contoh, turunan kedua ${\displaystyle {\tfrac {d^{2}y}{dx^{2}}}}$ memiliki dimensi yang sama dengan ${\displaystyle {\tfrac {y}{x^{2}}}}$.

Notasi Lagrange

Terkadang disebut dengan notasi petik/prima (prime notation),^[4] salah satu notasi turunan yang umum lainnya adalah notasi yang diperkenalkan Joseph-Louis Lagrange. Notasi ini menggunakan simbol prima, yang mirip dengan simbol petik. Turunan dari fungsi ${\displaystyle f}$ dituliskan sebagai ${\displaystyle f'}$. Serupa dengan itu, turunan kedua dan ketiga dari fungsi ditulis sebagai

${\displaystyle (f')'=f''}$   dan   ${\displaystyle (f'')'=f'''.}$

Untuk menyatakan turunan tingkat tinggi, beberapa penulis menggunakan angka Romawi yang ditulis sebagai tika atas, sedangkan yang lain menuliskan angka dalam simbol kurung:

${\displaystyle f^{\mathrm {iv} }}$   atau   ${\displaystyle f^{(4)}.}$

Notasi yang kedua dapat diperumum untuk menghasilkan notasi ${\displaystyle f^{(n)}}$ untuk turunan ke-n dari ${\displaystyle f}$. Notasi ini ringkas dan paling berguna ketika turunan dianggap sebagai fungsi tersendiri, berbeda dengan notasi Leibniz yang mengganggap turunan sebagai hubungan antar variabel. Nilai fungsi turunan ke-n di ${\displaystyle a}$ dituliskan sebagai ${\displaystyle f^{(n)}(a)}$.

Notasi Newton

Notasi Newton untuk turunan juga disebut sebagai notasi dot/titik. Notasi ini menggunakan titik yang diletakkan di atas nama fungsi, untuk merepresentasikan turunan terhadap waktu. Jika ${\displaystyle y=f(t)}$, maka

${\displaystyle {\dot {y}}}$   dan   ${\displaystyle {\ddot {y}}}$

masing-masing menyatakan turunan pertama dan turunan kedua dari ${\displaystyle y}$. Notasi Newton saat ini hanya digunakan untuk turunan terhadap waktu atau terhadap panjang busur, yang umum ditemukan dalam persamaan diferensial di fisika dan geometri diferensial.^[5][6] Notasi Newton, malangnya, sulit digunakan untuk turunan tingkat tinggi (turunan ke-4 atau lebih), dan tidak dapat digunakan untuk fungsi multivariabel.

Notasi Euler

Notasi yang diperkenalkan Leonhard Euler menggunakan operator diferensial ${\displaystyle D}$, yang ketika diterapkan pada sebuah fungsi ${\displaystyle f}$ akan menghasilkan turunan pertama ${\displaystyle Df}$. Turunan ke-n dengan notasi ini ditulis sebagai ${\displaystyle D^{n}f}$. Jika ${\displaystyle y=f(x)}$ adalah variabel terikat, maka tika bawah ${\displaystyle x}$ umum dilekatkan ke ${\displaystyle D}$ untuk memperjelas ${\displaystyle x}$ adalah variabel bebas. Notasi Euler selanjutnya dapat ditulis sebagai

${\displaystyle D_{x}y}$   atau  ${\displaystyle D_{x}f(x)}$,

walaupun tika bawah umumnya tidak digunakan jika konteks variabel ${\displaystyle x}$ dapat dipahami, contohnya ketika ${\displaystyle x}$ adalah satu-satunya variabel bebas dalam ekspresi. Notasi Euler berguna dalam menyatakan dan menyelesaikan sistem persamaan diferensial linear.

Kaidah dalam menentukan turunan fungsi

Definisi turunan dapat digunakan untuk menentukan turunan suatu fungsi, seperti ${\displaystyle x^{n}}$ dan ${\displaystyle \sin(x)}$. Proses ini dilakukan membuat persamaan perbandingan beda, lalu menghitung limitnya. Tapi pada praktiknya proses ini seringkali melelahkan. Dalam pendidikan terkait kalkulus diferensial, proses ini hanya dilakukan pada awal pembelajaran. Selanjutnya, menentukan turunan fungsi dilakukan dengan merujuk pada tabel/daftar turunan fungsi yang umum maupun dengan menggunakan aturan-aturan turunan.

Kaidah untuk fungsi-fungsi dasar

Setiap aturan pada bagian ini dapat dihasilkan dengan membuat persamaan beda, lalu menghitung limit ${\displaystyle h\to 0}$. Proses tersebut memerlukan strategi yang berbeda untuk mendapatkan hasil turunan, tergantung jenis fungsinya. Pada bagian ini, ${\displaystyle a}$ berupa bilangan real.

• Turunan pangkat:

  ${\displaystyle {\frac {d}{dx}}x^{a}=ax^{a-1}.}$

  ${\displaystyle {\frac {d}{dx}}x^{a}={\frac {d}{dx}}x\cdot a\cdot x^{a-1}}$

• Turunan implisit^[7]:

Contoh 1: mencari turunan dy/dx dari:

${\displaystyle x^{3}+3x+2=y^{2}}$

dapat dilakukan dengan cara berikut:

${\displaystyle \rightarrow \quad {\frac {d}{dx}}(x^{3}+3x+2)={\frac {d}{dx}}(y^{2})}$

${\displaystyle \rightarrow \quad {\frac {d}{dx}}x^{3}+{\frac {d}{dx}}3x+{\frac {d}{dx}}2={\frac {d}{dx}}y^{2}}$

${\displaystyle \rightarrow \quad 3x^{2}+3={\frac {d}{dx}}{\frac {dy}{dy}}y^{2}}$

${\displaystyle \rightarrow \quad 3x^{2}+3={\frac {dy}{dx}}{\frac {d}{dy}}y^{2}}$

${\displaystyle \rightarrow \quad 3x^{2}+3={\frac {dy}{dx}}2y}$

${\displaystyle \rightarrow \quad {\frac {dy}{dx}}={\frac {3x^{2}+3}{2y}}}$

Contoh 2: mencari turunan dx/dy dari:

${\displaystyle x^{3}+3x+2=y^{2}}$

dapat dilakukan dengan cara berikut:

${\displaystyle \rightarrow \quad {\frac {d}{dy}}x^{3}+{\frac {d}{dy}}3x+{\frac {d}{dy}}2={\frac {d}{dy}}y^{2}}$

${\displaystyle \rightarrow \quad {\frac {d}{dy}}{\frac {dx}{dx}}x^{3}+{\frac {d}{dy}}{\frac {dx}{dx}}3x=2y}$

${\displaystyle \rightarrow \quad {\frac {dx}{dy}}{\frac {d}{dx}}x^{3}+{\frac {dx}{dy}}{\frac {d}{dx}}3x=2y}$

${\displaystyle \rightarrow \quad {\frac {dx}{dy}}3x^{2}+{\frac {dx}{dy}}3=2y}$

${\displaystyle \rightarrow \quad {\frac {dx}{dy}}={\frac {2y}{3x^{2}+3}}}$

• Fungsi eksponensial dan logaritma:

  ${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}.}$

  ${\displaystyle {\frac {d}{dx}}a^{x}=a^{x}\ln(a),\qquad a>0}$

  ${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}},\qquad x>0.}$

  ${\displaystyle {\frac {d}{dx}}\log _{a}(x)={\frac {1}{x\ln(a)}},\qquad x,a>0}$

• Fungsi trigonometri:

  ${\displaystyle {\frac {d}{dx}}\sin(x)=\cos(x).}$

  ${\displaystyle {\frac {d}{dx}}\cos(x)=-\sin(x).}$

  ${\displaystyle {\frac {d}{dx}}\tan(x)=\sec ^{2}(x)={\frac {1}{\cos ^{2}(x)}}=1+\tan ^{2}(x).}$

• Fungsi invers trigonometri:

  ${\displaystyle {\frac {d}{dx}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.}$

  ${\displaystyle {\frac {d}{dx}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.}$

  ${\displaystyle {\frac {d}{dx}}\arctan(x)={\frac {1}{1+x^{2}}}}$

Kaidah untuk fungsi komposit

Beberapa aturan berikut dapat digunakan untuk menentukan turunan komposisi fungsi dengan membaginya menjadi masalah-masalah turunan yang lebih sederhana. Pada bagian ini, ${\displaystyle f}$, ${\displaystyle g}$, dan ${\displaystyle h}$ adalah fungsi yang terdiferensialkan pada selang ${\displaystyle I}$.

• Aturan konstanta:

  ${\displaystyle f'(x)=0.}$ untuk ${\displaystyle f(x)}$ berupa fungsi konstan.

• Kaidah jumlah:

  ${\displaystyle (\alpha f+\beta g)'=\alpha f'+\beta g'}$ untuk semua fungsi f dan g, dan untuk semua bilangan real ${\displaystyle \alpha }$ dan ${\displaystyle \beta }$.

• Kaidah darab:

  ${\displaystyle (f\cdot g)'=f'\cdot g+f\cdot g'}$ untuk semua fungsi f dan g. Aturan ini mencakup kasus yang istimewa, yakni fakta bahwa ${\displaystyle (\alpha \cdot f)'=\alpha \cdot f'}$ dengan ${\displaystyle \alpha }$ berupa konstanta. Karena menurut aturan konstanta, ${\displaystyle (\alpha \cdot f)'=\alpha \cdot f'+\alpha '\cdot f=\alpha \cdot f'+0\cdot f=\alpha \cdot f'}$.

• Kaidah hasil-bagi:

  ${\displaystyle \left({\frac {g}{h}}\right)'={\frac {g'\cdot h-g\cdot h'}{h^{2}}}}$ untuk semua fungsi ${\displaystyle g}$ dan ${\displaystyle h}$, di semua titik ${\displaystyle x}$ di ${\displaystyle I}$ yang memenuhi ${\displaystyle h(x)\neq 0}$. Pada kasus ${\displaystyle g}$ berupa fungsi konstan bernilai ${\displaystyle 1}$, akan didapatkan hubungan ${\displaystyle \left({\frac {1}{h}}\right)'={\frac {-h'}{h^{2}}}}$

• Aturan rantai untuk komposisi fungsi:

  Jika fungsi ${\displaystyle h}$ terdiferensialkan pada selang ${\displaystyle I_{1}}$, dan fungsi ${\displaystyle g}$ terdiferensialkan pada selang ${\displaystyle I_{2}=h(I_{1})}$ (${\displaystyle I_{2}}$ adalah citra dari ${\displaystyle I_{1}}$ yang dihasilkan fungsi ${\displaystyle h}$), maka komposisi fungsi ${\displaystyle g\circ h}$ terdiferensialkan di ${\displaystyle I_{1}}$ dan

  ${\displaystyle (g\circ h)'(x)=g'(h(x))\cdot h'(x).}$

• Kaidah fungsi invers:

  Jika fungsi ${\displaystyle f}$ bersifat bijektif, dan ${\displaystyle f^{-1}}$ adalah invers dari fungsi tersebut, maka

  ${\displaystyle [f^{-1}]'(x)={\frac {1}{f'(f^{-1}(x))}}}$

  Hubungan ini berlaku sembarang titik ${\displaystyle x}$ yang memenuhi ${\displaystyle f'(f^{-1}(x))\neq 0}$

Contoh perhitungan

Turunan dari fungsi

${\displaystyle f(x)=x^{4}+\sin \left(x^{2}\right)-\ln(x)e^{x}+7}$

dapat dilakukan dengan pertama kali menerapkan kaidah jumlah; turunan dari penjumlahan fungsi-fungsi sama dengan penjumlahan dari turunan fungsi-fungsi:

Tahap selanjutnya adalah menghitung turunan dari masing-masing fungsi. Kaidah rantai digunakan untuk menentukan turunan dari ${\displaystyle \cos(x^{2})}$, sedangkan kaidah darab digunakan untuk menentukan turunan ${\displaystyle \ln(x)e^{x}}$:

${\displaystyle {\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {d\left(x^{2}\right)}{dx}}\cos \left(x^{2}\right)-{\frac {d\left(\ln {x}\right)}{dx}}e^{x}-\ln(x){\frac {d\left(e^{x}\right)}{dx}}+0\\&=4x^{3}+2x\cos \left(x^{2}\right)-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}}$

Turunan tingkat tinggi

Misalkan ${\displaystyle f}$ adalah fungsi terdiferensialkan, dan ${\displaystyle f'}$ adalah fungsi turunannya. Turunan dari ${\displaystyle f'}$ (jika ada) ditulis sebagai ${\displaystyle f''}$ dan disebut turunan kedua dari ${\displaystyle f}$. Serupa dengan itu, turunan dari turunan kedua, jika ada, ditulis sebagai ${\displaystyle f'''}$ dan disebut turunan ketiga dari ${\displaystyle f}$; dan seterusnya. Turunan berulang ini disebut turunan tingkat tinggi. Turunan ke-n juga dapat dituliskan sebagai ${\displaystyle f^{(n)}}$. Jika ${\displaystyle x(t)}$ menyatakan posisi suatu objek pada waktu ${\displaystyle t}$, maka turunan tingkat tinggi dari ${\displaystyle x}$ memiliki interpretasi khusus dalam bidang fisika. Turunan pertama dari ${\displaystyle x}$ menyatakan kecepatan objek, turunan kedua menyatakan besar akselerasinya, sedangkan turunan ketiga dari ${\displaystyle x}$ menyatakan sentakan.

Fungsi mulus

Sebuah fungsi yang dapat diturunkan tak hingga kali disebut fungsi mulus. Tidak semua fungsi merupakan fungsi mulus; sebagai contoh, fungsi ${\displaystyle f}$ yang tidak kontinu tidak dapat diturunkan. Serupa dengan itu, bahkan jika ${\displaystyle f}$ memiliki turunan, fungsi turunan keduanya mungkin tidak ada. Sebagai contoh, misalkan fungsi

${\displaystyle f(x)={\begin{cases}+x^{2},&{\text{jika }}x\geq 0\\-x^{2},&{\text{jika }}x\leq 0.\end{cases}}}$

Perhitungan menunjukkan bahwa ${\displaystyle f'(x)=2|x|}$ adalah fungsi yang terdiferensialkan namun tidak memiliki turunan di nol. Jika suatu fungsi dapat diturunkan k kali berturut-turut dan turunan ke-k-nya bersifat kontinu, maka fungsi tersebut merupakan anggota kelas keterdiferensialan C^k.

Polinomial Taylor dengan sisa

Pada garis bilangan real, setiap fungsi polinomial terdiferensialkan tak hingga kali. Dengan menggunakan kaidah turunan pangkat, sebuah polinomial berderajat n akan menjadi fungsi konstan jika diturunkan sebanyak n kali. Semua turunan fungsi tersebut selanjutnya sama dengan 0 (fungsi konstan). Hal ini mengartikan fungsi polinomial termasuk fungsi mulus.

Turunan tingkat tinggi dari sebuah fungsi ${\displaystyle f}$ di suatu titik ${\displaystyle x}$, akan memberikan hampiran polinomial terbaik untuk fungsi tersebut di sekitar titik ${\displaystyle x}$. Sebagai contoh, jika ${\displaystyle f}$ terdiferensialkan dua kali, maka

${\displaystyle f(x+h)\approx f(x)+f'(x)h+{\tfrac {1}{2}}f''(x)h^{2}}$

dalam artian bahwa

${\displaystyle \lim _{h\to 0}{\frac {f(x+h)-f(x)-f'(x)h-{\frac {1}{2}}f''(x)h^{2}}{h^{2}}}=0.}$

Jika ${\displaystyle f}$ terdiferensialkan tak hingga kali, maka persamaan turunan kedua dapat diteruskan menjadi deret Taylor untuk fungsi ${\displaystyle f}$ yang dievaluasi di x + h sekitar titik x.

Kaidah untuk turunan tingkat tinggi

• Aturan Leibniz

  Jika ${\displaystyle f}$ dan ${\displaystyle g}$ dapat diturunkan sebanyak ${\displaystyle n}$ kali, maka turunan ke-${\displaystyle n}$ dari fungsi ${\displaystyle f(x)\cdot g(x)}$ adalah

  ${\displaystyle (fg)^{(n)}=\sum _{k=0}^{n}{\binom {n}{k}}f^{(k)}g^{(n-k)}.}$

  Ekspresi ${\textstyle {\binom {n}{k}}}$ yang muncul pada persamaan tersebut menandakan koefisien binomial. Aturan ini adalah perumuman dari kaidah darab.

Turunan pada sistem bilangan kompleks

Definisi dan aturan-aturan terkait turunan dapat diperumum untuk fungsi dengan variabel kompleks dan nilai kompleks. Perumuman ini dapat dilakukan karena bilangan kompleks juga memiliki sifat penjumlahan, perkalian, dan pembagian; sama seperti bilangan real. Selain itu, konsep jarak (Euklides) antar bilangan pada bilangan kompleks dapat dijelaskan secara sederhana.

Jika ${\displaystyle U\subset \mathbb {C} }$ berupa himpunan buka, dan ${\displaystyle f:U\to \mathbb {C} }$ adalah fungsi bernilai kompleks, maka ${\displaystyle f}$ dikatakan terdiferensialkan di titik ${\displaystyle z\in \mathbb {C} }$ bila nilai limit

${\displaystyle \lim _{h\to 0}{\frac {f(z+h)-f(z)}{h}}}$

ada.^[8] Turunan kompleks ini disimbolkan dengan ${\displaystyle f'(z).}$ Definisi ini memungkinkan untuk menggunakan konsep kelinearan: turunan menyatakan besar "kemiringan" dari fungsi [kompleks] linear terbaik yang menghampiri fungsi ${\displaystyle f.}$ Tapi, perhatian lebih diperlukan karena nilai ${\displaystyle h}$ pada limit berupa bilangan kompleks. Berbeda dengan limit pada bilangan real yang hanya memerlukan dua arah ("limit dari kanan" dan "limit dari kiri"), limit pada bilangan kompleks dapat "bergerak" dari takhingga banyaknya arah. Akibatnya, konsep turunan fungsi kompleks jauh lebih ketat ketimbang pada fungsi bernilai real. Sebagai contoh fungsi nilai mutlak kompleks tidak memiliki turunan dimanapun. Sebuah fungsi kompleks dapat diturunkan pada suatu titik, jika dan hanya jika fungsi tersebut memenuhi persamaan Cauchy-Riemann di titik tersebut.

Walaupun (atau tepatnya karena) konsep turunan yang jauh lebih ketat, aturan-aturan perhitungan turunan pada fungsi bilangan real dapat digunakan untuk fungsi bilangan kompleks. Hal ini mencakup aturan jumlah, darab, dan rantai, juga aturan fungsi invers. Banyak fungsi kompleks, seperti eksponensial dan logaritma, memiliki sifat turunan yang mirip dengan versi realnya.

Jika fungsi ${\displaystyle f}$ terdiferensialkan di keseluruhan domain ${\displaystyle U}$, maka fungsi ${\displaystyle f}$ disebut fungsi holomorfik di ${\displaystyle U}$.^[9] Fungsi kompleks yang terdiferensialkan di keseluruhan ${\displaystyle \mathbb {C} }$ disebut fungsi entire. Fungsi holomorfik memiliki beberapa sifat yang unik. Sebagai contoh, teorema Picard menyimpulkan bahwa citra (range) dari fungsi entire hanya dapat berupa: ${\displaystyle \mathbb {C} }$, ${\displaystyle \mathbb {C} \setminus \{z_{0}\}}$, atau ${\displaystyle \{z_{0}\}}$ untuk suatu ${\displaystyle z_{0}\in \mathbb {C} }$. Hasil ini dapat digunakan untuk menyimpulkan bahwa, jika fungsi kompleks ${\displaystyle f}$ tidak pernah menghasilkan nilai ${\displaystyle z}$ maupun nilai ${\displaystyle w}$, maka ${\displaystyle f}$ adalah fungsi konstan.

Turunan untuk fungsi bernilai vektor

Sebuah fungsi bernilai vektor ${\displaystyle \mathbf {y} }$ dengan variabel real, adalah fungsi yang memetakan bilangan real (ril) ke suatu vektor di suatu ruang vektor ${\displaystyle \mathbb {R} ^{n}}$. Fungsi bernilai vektor dapat dibagi menjadi fungsi-fungsi koordinatnya, ${\displaystyle y_{1}(t),\,y_{2}(t),\,\dots ,\,y_{n}(t)}$. Hal ini mengartikan fungsi ${\displaystyle \mathbf {y} }$ dapat ditulis sebagai ${\displaystyle \mathbf {y} (t)=(y_{1}(t),\,y_{2}(t),\,\dots ,\,y_{n}(t))}$. Contoh dari fungsi bernilai vektor adalah kurva parametrik di ${\displaystyle \mathbb {R} ^{2}}$ atau ${\displaystyle \mathbb {R} ^{3}}$. Fungsi-fungsi koordinat adalah fungsi bernilai real, mengakibatkan definisi turunan dapat diterapkan bagi mereka semua. Turunan dari fungsi ${\displaystyle \mathbf {y} (t)}$ didefinisikan sebagai sebuah vektor, disebut vektor singgung, yang koordinatnya adalah nilai turunan dari semua fungsi koordinatnya. Dengan kata lain,

Bentuk tersebut dapat dihasilkan dari menghitungdengan mengasumsikan limit dari fungsi tersebut ada. Sebagai contoh, bila ${\displaystyle \mathbf {y} (t)}$ adalah vektor yang menandakan posisi suatu partikel pada waktu ${\displaystyle t}$, turunan ${\displaystyle \mathbf {y} '(t)}$ dapat dipandang sebagai vektor kecepatan dari partikel pada waktu ${\displaystyle t}$.

Turunan untuk fungsi multivariabel

Pembahasan pada bagian-bagian sebelumnya hanya memperhatikan fungsi dengan satu variabel. Fungsi yang memetakan vektor ke vektor maupun vektor ke bilangan juga dapat memiliki turunan. Tetapi, garis singgung pada grafik fungsi tersebut belum tentu unik, karena ada banyak arah yang mungkin untuk membuat garis tersebut. Oleh karena itu, perumuman turunan diperlukan untuk jenis fungsi ini.

Keterdiferensialan dan matriks Jacobi

Turunan parsial