アポロニウスの円

アポロニウスの円（アポロニウスのえん）は、2定点A・Bをとり、点PをAP:BPが一定となるように（但しAP≠BP）したときの点Pの軌跡である。ペルガのアポロニウスの名前を残すが、起源はより古いと思われる。例えば、既にアリストテレス『気象論』第三巻で虹の形状を論じるのに用いられている。

証明

初等幾何による証明

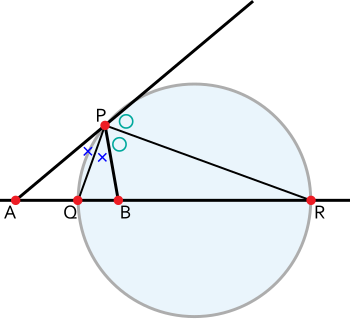
点PをAP:BPが一定となるようにしたときの点Pの軌跡のうち、線分ABの上の点をQ、ABの延長線上の点をRとすると、

AQ:QB=AP:PB

AR:RB=AP:PB

内角と外角の二等分線の関係の逆より、PQとPRはそれぞれ∠APBの内角と外角の二等分線である。 よって、∠QPR=90° ゆえに、点Pの軌跡は線分QRを直径とする円である。

ベクトルによる証明（1）

m, n を互いに異なる正の実数とする。線分ABを m ： n に内分する点を Q、外分する点をRとすると、

${\displaystyle {\overrightarrow {\mathrm {PQ} }}={\frac {n{\overrightarrow {\mathrm {PA} }}+m{\overrightarrow {\mathrm {PB} }}}{n+m}},\ {\overrightarrow {\mathrm {PR} }}={\frac {n{\overrightarrow {\mathrm {PA} }}-m{\overrightarrow {\mathrm {PB} }}}{n-m}}.}$

このとき、

${\displaystyle \mathrm {PA} :\mathrm {PB} =m:n.}$

${\displaystyle \Leftrightarrow n|{\overrightarrow {\mathrm {PA} }}|=m|{\overrightarrow {\mathrm {PB} }}|.}$

${\displaystyle \Leftrightarrow n^{2}|{\overrightarrow {\mathrm {PA} }}|^{2}=m^{2}|{\overrightarrow {\mathrm {PB} }}|^{2}.}$

${\displaystyle \Leftrightarrow (n{\overrightarrow {\mathrm {PA} }}+m{\overrightarrow {\mathrm {PB} }})\cdot (n{\overrightarrow {\mathrm {PA} }}-m{\overrightarrow {\mathrm {PB} }})=0.}$

${\displaystyle \Leftrightarrow {\frac {n{\overrightarrow {\mathrm {PA} }}+m{\overrightarrow {\mathrm {PB} }}}{n+m}}\cdot {\frac {n{\overrightarrow {\mathrm {PA} }}-m{\overrightarrow {\mathrm {PB} }}}{n-m}}=0.}$

${\displaystyle \Leftrightarrow {\overrightarrow {\mathrm {PQ} }}\cdot {\overrightarrow {\mathrm {PR} }}=0.}$

${\displaystyle \Leftrightarrow {\overrightarrow {\mathrm {PQ} }}={\vec {0}}\vee {\overrightarrow {\mathrm {PR} }}={\vec {0}}\vee {\overrightarrow {\mathrm {PQ} }}\perp {\overrightarrow {\mathrm {PR} }}.}$

${\displaystyle \Leftrightarrow \mathrm {P} =\mathrm {Q} \vee \mathrm {P} =\mathrm {R} \vee \angle {\mathrm {QPR} }=90^{\circ }.}$

したがって、点Pの軌跡は線分QRを直径とする円になる。

ベクトルによる証明（2）

線分QRの中点をOとすると、

${\displaystyle {\overrightarrow {\mathrm {OQ} }}=-{\frac {1}{2}}{\overrightarrow {\mathrm {QR} }},\ {\overrightarrow {\mathrm {OR} }}={\frac {1}{2}}{\overrightarrow {\mathrm {QR} }}.}$

したがって、

${\displaystyle {\overrightarrow {\mathrm {PQ} }}\cdot {\overrightarrow {\mathrm {PR} }}=0.}$

${\displaystyle \Leftrightarrow ({\overrightarrow {\mathrm {PO} }}+{\overrightarrow {\mathrm {OQ} }})\cdot ({\overrightarrow {\mathrm {PO} }}+{\overrightarrow {\mathrm {OR} }})=0.}$

${\displaystyle \Leftrightarrow ({\overrightarrow {\mathrm {PO} }}-{\frac {1}{2}}{\overrightarrow {\mathrm {QR} }})\cdot ({\overrightarrow {\mathrm {PO} }}+{\frac {1}{2}}{\overrightarrow {\mathrm {QR} }})=0.}$

${\displaystyle \Leftrightarrow |{\overrightarrow {\mathrm {PO} }}|^{2}=\left({\frac {1}{2}}\right)^{2}|{\overrightarrow {\mathrm {QR} }}|^{2}.}$

${\displaystyle \Leftrightarrow \mathrm {PO} ={\frac {1}{2}}\mathrm {QR} .}$

これより、点Pの軌跡は線分QRの中点Oを中心とする半径 ${\displaystyle {\frac {1}{2}}\mathrm {QR} }$ の円、すなわち線分QRを直径とする円になる。

アポロニウスの円の中心

線分QRの中点をOとすると、点Oはアポロニウスの円の中心となり、

${\displaystyle {\begin{aligned}{\overrightarrow {\mathrm {PO} }}&={\frac {{\overrightarrow {\mathrm {PQ} }}+{\overrightarrow {\mathrm {PR} }}}{2}}\\&={\frac {1}{2}}\left({\frac {n{\overrightarrow {\mathrm {PA} }}+m{\overrightarrow {\mathrm {PB} }}}{n+m}}+{\frac {n{\overrightarrow {\mathrm {PA} }}-m{\overrightarrow {\mathrm {PB} }}}{n-m}}\right)\\&={\frac {(n-m)(n{\overrightarrow {\mathrm {PA} }}+m{\overrightarrow {\mathrm {PB} }})+(n+m)(n{\overrightarrow {\mathrm {PA} }}-m{\overrightarrow {\mathrm {PB} }})}{2(n+m)(n-m)}}\\&={\frac {2n^{2}{\overrightarrow {\mathrm {PA} }}-2m^{2}{\overrightarrow {\mathrm {PB} }}}{2(n^{2}-m^{2})}}\\&={\frac {n^{2}{\overrightarrow {\mathrm {PA} }}-m^{2}{\overrightarrow {\mathrm {PB} }}}{n^{2}-m^{2}}}.\end{aligned}}}$

すなわち、点Oは線分ABを ${\displaystyle m^{2}:n^{2}}$ に外分する点になる。

アポロニウスの円の半径

アポロニウスの円の半径を r とする。ここで平方完成

${\displaystyle {\begin{aligned}{\frac {1}{2}}{\overrightarrow {\mathrm {QR} }}&={\frac {{\overrightarrow {\mathrm {PR} }}-{\overrightarrow {\mathrm {PQ} }}}{2}}\\&={\frac {1}{2}}\left({\frac {n{\overrightarrow {\mathrm {PA} }}-m{\overrightarrow {\mathrm {PB} }}}{n-m}}-{\frac {n{\overrightarrow {\mathrm {PA} }}+m{\overrightarrow {\mathrm {PB} }}}{n+m}}\right)\\&={\frac {(n+m)(n{\overrightarrow {\mathrm {PA} }}-m{\overrightarrow {\mathrm {PB} }})-(n-m)(n{\overrightarrow {\mathrm {PA} }}+m{\overrightarrow {\mathrm {PB} }})}{2(n+m)(n-m)}}\\&={\frac {2mn{\overrightarrow {\mathrm {PA} }}-2mn{\overrightarrow {\mathrm {PB} }}}{2(n^{2}-m^{2})}}\\&={\frac {mn({\overrightarrow {\mathrm {PB} }}-{\overrightarrow {\mathrm {PA} }})}{m^{2}-n^{2}}}\\&={\frac {mn}{m^{2}-n^{2}}}{\overrightarrow {\mathrm {AB} }}.\end{aligned}}}$

定義より、

${\displaystyle {\begin{aligned}{\overrightarrow {\mathrm {AR} }}&={\overrightarrow {\mathrm {PR} }}-{\overrightarrow {\mathrm {PA} }}\\&={\frac {n{\overrightarrow {\mathrm {PA} }}-m{\overrightarrow {\mathrm {PB} }}}{n-m}}-{\overrightarrow {\mathrm {PA} }}\\&={\frac {m}{n-m}}({\overrightarrow {\mathrm {PA} }}-{\overrightarrow {\mathrm {PB} }})\\&={\frac {m}{m-n}}{\overrightarrow {\mathrm {AB} }},\\{\overrightarrow {\mathrm {QB} }}&={\frac {n}{m+n}}{\overrightarrow {\mathrm {AB} }},\\{\overrightarrow {\mathrm {AO} }}&={\overrightarrow {\mathrm {PO} }}-{\overrightarrow {\mathrm {PA} }}\\&={\frac {n^{2}{\overrightarrow {\mathrm {PA} }}-m^{2}{\overrightarrow {\mathrm {PB} }}}{n^{2}-m^{2}}}-{\overrightarrow {\mathrm {PA} }}\\&={\frac {m^{2}}{n^{2}-m^{2}}}({\overrightarrow {\mathrm {PA} }}-{\overrightarrow {\mathrm {PB} }})\\&={\frac {m^{2}}{m^{2}-n^{2}}}{\overrightarrow {\mathrm {AB} }},\\{\overrightarrow {\mathrm {BO} }}&={\overrightarrow {\mathrm {PO} }}-{\overrightarrow {\mathrm {PB} }}\\&={\frac {n^{2}{\overrightarrow {\mathrm {PA} }}-m^{2}{\overrightarrow {\mathrm {PB} }}}{n^{2}-m^{2}}}-{\overrightarrow {\mathrm {PB} }}\\&={\frac {n^{2}}{n^{2}-m^{2}}}({\overrightarrow {\mathrm {PA} }}-{\overrightarrow {\mathrm {PB} }})\\&={\frac {n^{2}}{m^{2}-n^{2}}}{\overrightarrow {\mathrm {AB} }}.\end{aligned}}}$

したがって、

${\displaystyle r=\left|{\frac {mn}{m^{2}-n^{2}}}\right|\cdot \mathrm {AB} ={\frac {\mathrm {AR} \cdot \mathrm {QB} }{\mathrm {AB} }}={\sqrt {\mathrm {OA} \cdot \mathrm {OB} }}.}$

アポロニウスの問題に対する解

アポロニウスの問題に対する解はアポロニウスの円とも呼ばれる。

外部リンク

• アポロニウスの円の中心について - 『数研通信』33号
• アポロニウスの円の中心と半径
• アポロニウスの円～定義を少し広げる試み～
• 高校数学で注意して欲しいこと　2. 軌跡
• 角の二等分線の性質を狩る
• 『アポロニウスの円の証明と応用』 - 高校数学の美しい物語
• アポロニウスの接円問題の探究 - 筑波大学数学教育研究室 代数・幾何・微積　For All プロジェクト