弾性率

弾性率（だんせいりつ、英語: elastic modulus）は、変形のしにくさを表す物性値であり、弾性変形における応力とひずみの間の比例定数の総称である。弾性係数あるいは弾性定数とも呼ばれる[1]。

1807年にトマス・ヤングによって導入された[2]。

種類

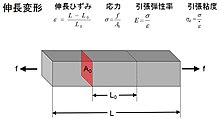単純な伸長変形のモデル。L_0は元長、Lは変形後長さ、εは伸長ひずみ、fは力、A_0は変形前における力と垂直な断面積、σは応力、Eは伸長弾性率、η_Eは伸長粘度、上にドットの付いたεは伸長ひずみの時間微分である。
単純な剪断変形のモデル。dは変位、hは力と垂直な厚さ、αは倒れ角、γは剪断ひずみ、fは力、A_0は変形前における力と平行な断面積、σは応力、Gは剪断弾性率、ηは剪断粘度、上にドットの付いたγは剪断ひずみの時間微分である。
単純な体積変形のモデル。V_0は元体積、Vは変形後体積、κは体積ひずみ、fは力、A_0は変形前における表面積、σは応力、Kは体積弾性率、η_Vは体積粘度、上にドットの付いたκは体積ひずみの時間微分である。

弾性率は、弾性変形における応力とひずみの間の比例定数(応力/ひずみ)であり、加えられた外力(応力)を分子、応力によって引き起こされたひずみを分母とした商である[3]。

弾性率 = 応力/ひずみ

ひずみは無次元であるので、弾性率は応力と同じ次元を持ち、SIにおける単位はパスカル（記号: Pa）、ニュートン毎平方メートル（記号: N/m2）が用いられる。また、弾性率の逆数を弾性コンプライアンス定数や単に弾性コンプライアンスという。単位は1/Pa、m2/N。

弾性変形は伸長(または圧縮)変形、剪断変形、体積変形の3つの種類に分けられ、従って弾性率も3種類ある。それぞれひずみの定義は異なる。

  • 引張弾性率 E {\displaystyle E} ：引張力や圧縮力などの単軸応力についての弾性率。ヤング率（縦弾性係数）。
E = σ ε {\displaystyle E={\frac {\sigma }{\varepsilon }}}
伸長ひずみ ε = L − L 0 L 0 {\displaystyle \varepsilon ={\frac {L-L_{0}}{L_{0}}}} （ L 0 {\displaystyle L_{0}} は元々の長さ、 L {\displaystyle L} は引張後長さ）
伸長粘度 η E = σ d ε / d t {\displaystyle \eta _{E}={\frac {\sigma }{d\varepsilon /dt}}} （tは時間）
  • 剪断弾性率 G {\displaystyle G} ：せん断力についての弾性率。剛性率（ずり弾性率・横弾性係数・せん断弾性係数・ラメの第二定数）。
G = σ γ {\displaystyle G={\frac {\sigma }{\gamma }}}
剪断ひずみ γ = d h = tan ⁡ α {\displaystyle \gamma ={\frac {d}{h}}=\tan \alpha } （ d {\displaystyle d} は剪断により面が剪断力方向に移動した距離、 h {\displaystyle h} は剪断力方向と垂直な試料厚さ、 α {\displaystyle \alpha } は、試料の面が長方形から平行四辺形になるときの倒れ角）
剪断粘度 η = σ d γ / d t {\displaystyle \eta ={\frac {\sigma }{d\gamma /dt}}}
K = σ κ {\displaystyle K={\frac {\sigma }{\kappa }}}
体積ひずみ κ = V − V 0 V 0 {\displaystyle \kappa ={\frac {V-V_{0}}{V_{0}}}} （ V 0 {\displaystyle V_{0}} は元々の体積、 V {\displaystyle V} は変形後体積）
体積粘度 η V = σ d κ / d t {\displaystyle \eta _{V}={\frac {\sigma }{d\kappa /dt}}}

テンソル量としての弾性率

2階のテンソル量である応力σとひずみεに対して、弾性率Dは4階のテンソル量で表すことができる[4]。

σ = D ϵ , {\displaystyle {\boldsymbol {\sigma }}={\boldsymbol {D}}{\boldsymbol {\epsilon }},}
σ i j = D i j k l ϵ k l ( i , j , k , l = 1 ∼ 3 ) {\displaystyle \sigma _{ij}=D_{ijkl}\epsilon _{kl}\quad (i,j,k,l=1\sim 3)} [5]

弾性率はテンソルであるため、物質客観性の原理により座標変換においてσ=Dεの関係を保たねばならない。座標系O-x1x2x3からO-x '1x '2x '3へ変換するとき、弾性率テンソルの成分は

D i j m n ′ = D p q r s l i p l j q l m r l n s {\displaystyle D'_{ijmn}=D_{pqrs}l_{ip}l_{jq}l_{mr}l_{ns}}

と変換される[6]。ここでlipは、xi軸とx'p軸の方向余弦である。

弾性率テンソルは81(= 34)個の成分を持つが、応力テンソルσとひずみテンソルεは対称性、すなわち

σ i j = σ j i , ϵ i j = ϵ j i {\displaystyle \sigma _{ij}=\sigma _{ji},\quad \epsilon _{ij}=\epsilon _{ji}}

によりそれぞれ独立な6成分を持つので、弾性率テンソルDも

D i j k l = D j i l k {\displaystyle D_{ijkl}=D_{jilk}}

の性質を持ち、独立な成分は36(= 62)個となる。さらに単位体積あたりの弾性ひずみエネルギー

d W ≡ σ i j d ϵ i j {\displaystyle dW\equiv \sigma _{ij}\,d\epsilon _{ij}}

を用いて弾性率が

D i j k l = ∂ 2 W ∂ ϵ i j ∂ ϵ k l {\displaystyle D_{ijkl}={\frac {\partial ^{2}W}{\partial \epsilon _{ij}\partial \epsilon _{kl}}}}

と表せることから

D i j k l = D k l i j {\displaystyle D_{ijkl}=D_{klij}}

が成り立つため、最終的に弾性率テンソルDの独立な成分は21(= 6×(6+1)/2)個となる[6]。

等方均質材料の弾性率の相関関係

一般に、等方性物質（無定形ポリマー、非晶性・無配向ポリマーなど）では3種の弾性率（引張弾性率 E {\displaystyle E} 、剪断弾性率 G {\displaystyle G} 、体積弾性率 K {\displaystyle K} ）の関係について次式が成り立つ[3]。

E = 2 G ( 1 − ν ) = 3 K ( 1 − 2 ν ) {\displaystyle E=2G(1-\nu )=3K(1-2\nu )}

ここで、 ν {\displaystyle \nu } とは、縦方向のひずみと横方向のひずみとの比(ポアソン比)である。結晶性ポリマー、繊維、フィルム、繊維充填複合材料、一般の射出成形物などは等方性物質ではない。高分子鎖、充填繊維、結晶相などに配向を持ち、その程度は内部と表面で異なる。これ異方性物質は、独立した2つ以上の弾性率を持つ[7]。

材料が等方均質弾性材料とすると、弾性率テンソルD の独立な成分は2個まで絞られ[4]、次式のように書ける[8]。

D i j k l = λ δ i j δ k l + G ( δ i k δ j l + δ i l δ j k ) {\displaystyle D_{ijkl}=\lambda \delta _{ij}\delta _{kl}+G(\delta _{ik}\delta _{jl}+\delta _{il}\delta {jk})}

ここでδはクロネッカーのデルタである。

この場合、ヤング率E 、ポアソン比ν、体積弾性率K 、剛性率G 、ラメの第一定数λの5つの弾性率はそれぞれ、2つを用いて残りの3つを表すことができる。その関係を下に示す。ここで、α = (E2 + 9λ2 + 2E λ)1/2 とする。

等方均質弾性体における各弾性率間の変換式
E {\displaystyle E} （ヤング率） ν {\displaystyle \nu } （ポアソン比） K {\displaystyle K} （体積弾性率） G {\displaystyle G} （剛性率） λ {\displaystyle \lambda } （ラメの第一定数）
E , ν {\displaystyle E,\nu } E {\displaystyle E} ν {\displaystyle \nu } E 3 ( 1 − 2 ν ) {\displaystyle {\dfrac {E}{3(1-2\nu )}}} E 2 ( 1 + ν ) {\displaystyle {\dfrac {E}{2(1+\nu )}}} E ν ( 1 + ν ) ( 1 − 2 ν ) {\displaystyle {\dfrac {E\nu }{(1+\nu )(1-2\nu )}}}
E , K {\displaystyle E,K} E {\displaystyle E} 3 K − E 6 K {\displaystyle {\dfrac {3K-E}{6K}}} K {\displaystyle K} 3 K E 9 K − E {\displaystyle {\dfrac {3KE}{9K-E}}} 3 K ( 3 K − E ) 9 K − E {\displaystyle {\dfrac {3K(3K-E)}{9K-E}}}
E , G {\displaystyle E,G} E {\displaystyle E} E − 2 G 2 G {\displaystyle {\dfrac {E-2G}{2G}}} G E 3 ( 3 G − E ) {\displaystyle {\dfrac {GE}{3(3G-E)}}} G {\displaystyle G} G ( E − 2 G ) 3 G − E {\displaystyle {\dfrac {G(E-2G)}{3G-E}}}
E , λ {\displaystyle E,\lambda } E {\displaystyle E} 2 λ E + λ + α {\displaystyle {\dfrac {2\lambda }{E+\lambda +\alpha }}} E + 3 λ + α 6 {\displaystyle {\dfrac {E+3\lambda +\alpha }{6}}} E − 3 λ + α 4 {\displaystyle {\dfrac {E-3\lambda +\alpha }{4}}} λ {\displaystyle \lambda }
ν , K {\displaystyle \nu ,K} 3 K ( 1 − 2 ν ) {\displaystyle 3K(1-2\nu )} ν {\displaystyle \nu } K {\displaystyle K} 3 K ( 1 − 2 ν ) 2 ( 1 + ν ) {\displaystyle {\dfrac {3K(1-2\nu )}{2(1+\nu )}}} 3 K ν 1 + ν {\displaystyle {\dfrac {3K\nu }{1+\nu }}}
ν , G {\displaystyle \nu ,G} 2 G ( 1 + ν ) {\displaystyle 2G(1+\nu )} ν {\displaystyle \nu } 2 G ( 1 + ν ) 3 ( 1 − 2 ν ) {\displaystyle {\dfrac {2G(1+\nu )}{3(1-2\nu )}}} G {\displaystyle G} 2 G ν 1 − 2 ν {\displaystyle {\dfrac {2G\nu }{1-2\nu }}}
ν , λ {\displaystyle \nu ,\lambda } λ ( 1 + ν ) ( 1 − 2 ν ) ν {\displaystyle {\dfrac {\lambda (1+\nu )(1-2\nu )}{\nu }}} ν {\displaystyle \nu } λ ( 1 + ν ) 3 ν {\displaystyle {\dfrac {\lambda (1+\nu )}{3\nu }}} λ ( 1 − 2 ν ) 2 ν {\displaystyle {\dfrac {\lambda (1-2\nu )}{2\nu }}} λ {\displaystyle \lambda }
K , G {\displaystyle K,G} 9 K G 3 K + G {\displaystyle {\dfrac {9KG}{3K+G}}} 3 K − 2 G 6 K + 2 G {\displaystyle {\dfrac {3K-2G}{6K+2G}}} K {\displaystyle K} G {\displaystyle G} K − 2 3 G {\displaystyle K-{\frac {2}{3}}G}
K , λ {\displaystyle K,\lambda } 9 ( K − λ ) 3 K − λ {\displaystyle {\dfrac {9(K-\lambda )}{3K-\lambda }}} λ 3 K − λ {\displaystyle {\dfrac {\lambda }{3K-\lambda }}} K {\displaystyle K} 3 2 ( K − λ ) {\displaystyle {\frac {3}{2}}(K-\lambda )} λ {\displaystyle \lambda }
G , λ {\displaystyle G,\lambda } G ( 3 λ + 2 G ) λ + G {\displaystyle {\dfrac {G(3\lambda +2G)}{\lambda +G}}} λ 2 λ + 2 G {\displaystyle {\dfrac {\lambda }{2\lambda +2G}}} 3 λ + 2 G 3 {\displaystyle {\dfrac {3\lambda +2G}{3}}} G {\displaystyle G} λ {\displaystyle \lambda }

複素弾性率

詳細は「粘弾性#複素弾性率」を参照
「動的弾性率」も参照

粘弾性体に対しては、弾性率は複素数で表される。複素弾性率の実部は貯蔵弾性率、虚部は損失弾性率と呼ばれる。

脚注

[脚注の使い方]
  1. ^ 日本機械学会 編『機械工学辞典』（第2版）丸善、2007年、816頁。ISBN 978-4-88898-083-8。 
  2. ^ 小林英男; 轟章『固体の弾塑性力学』数理工学社、2007年、14頁。ISBN 978-4-901683-51-7。 
  3. ^ a b 中前勝彦 (Nov 1988). “入門講座　弾性率および粘弾性”. 高分子 37 (11): 826-829. doi:10.1295/kobunshi.37.826. https://doi.org/10.1295/kobunshi.37.826. 
  4. ^ a b 吉川弘道. “構成方程式の基本知識―考え方と定式化―” (PDF). 2020年4月26日閲覧。
  5. ^ 総和規約を用いており、総和記号が省略されていることに注意。
  6. ^ a b 中曽根祐司 編『異方性材料の弾性論』コロナ社、2014年、80-83頁。ISBN 978-4-339-04633-5。 
  7. ^ L. E. Nielsen：小野木重治 訳 (1980). 高分子と複合材料の力学的性質. 化学同人. pp. 26 
  8. ^ 井田喜明『自然災害のシミュレーション入門』朝倉書店、2014年、14頁。ISBN 978-4-254-16068-0。 

関連項目