後退微分法

後退微分法（こうたいびぶんほう、英: backward differentiation formula; BDF）は常微分方程式の数値解法の一つである。線型多段法の一種で、過去の複数の値を用いて現在値を計算する方法である。特に硬い微分方程式（英語版）の解を計算するときに使われている。

定義

常微分方程式とその初期値問題を次のように定める。

y ′ = f ( t , y ) , y ( t 0 ) = y 0 . {\displaystyle y'=f(t,y),\quad y(t_{0})=y_{0}.}

一般的に、BDFは次の形で表される[1]。

∑ k = 0 s a k y n + k = h β f ( t n + s , y n + s ) . {\displaystyle \sum _{k=0}^{s}a_{k}y_{n+k}=h\beta f(t_{n+s},y_{n+s}).}

ここで、h は時間の刻み幅で、 t n = t 0 + n h {\displaystyle t_{n}=t_{0}+nh} は離散化した時間であり、係数 a k {\displaystyle a_{k}} と β {\displaystyle \beta } は方法の次数を最大化するために選択される。s段法の場合、最大次数は s である。

BDF方法はすべて陰公式のため、一時刻ごとに（一般的な）非線形方程式系を解く必要がある。陰公式を解くためにはニュートン法のような反復法がよく用いられる。

公式

s段BDF方法（s < 7)は次通り[2]：

  • BDF1: y n + 1 − y n = h f ( t n + 1 , y n + 1 ) {\displaystyle y_{n+1}-y_{n}=hf(t_{n+1},y_{n+1})} ; (後退オイラー法)
  • BDF2: y n + 2 − 4 3 y n + 1 + 1 3 y n = 2 3 h f ( t n + 2 , y n + 2 ) ; {\displaystyle y_{n+2}-{\tfrac {4}{3}}y_{n+1}+{\tfrac {1}{3}}y_{n}={\tfrac {2}{3}}hf(t_{n+2},y_{n+2});}
  • BDF3: y n + 3 − 18 11 y n + 2 + 9 11 y n + 1 − 2 11 y n = 6 11 h f ( t n + 3 , y n + 3 ) {\displaystyle y_{n+3}-{\tfrac {18}{11}}y_{n+2}+{\tfrac {9}{11}}y_{n+1}-{\tfrac {2}{11}}y_{n}={\tfrac {6}{11}}hf(t_{n+3},y_{n+3})}
  • BDF4: y n + 4 − 48 25 y n + 3 + 36 25 y n + 2 − 16 25 y n + 1 + 3 25 y n = 12 25 h f ( t n + 4 , y n + 4 ) {\displaystyle y_{n+4}-{\tfrac {48}{25}}y_{n+3}+{\tfrac {36}{25}}y_{n+2}-{\tfrac {16}{25}}y_{n+1}+{\tfrac {3}{25}}y_{n}={\tfrac {12}{25}}hf(t_{n+4},y_{n+4})}
  • BDF5: y n + 5 − 300 137 y n + 4 + 300 137 y n + 3 − 200 137 y n + 2 + 75 137 y n + 1 − 12 137 y n = 60 137 h f ( t n + 5 , y n + 5 ) {\displaystyle y_{n+5}-{\tfrac {300}{137}}y_{n+4}+{\tfrac {300}{137}}y_{n+3}-{\tfrac {200}{137}}y_{n+2}+{\tfrac {75}{137}}y_{n+1}-{\tfrac {12}{137}}y_{n}={\tfrac {60}{137}}hf(t_{n+5},y_{n+5})}
  • BDF6: y n + 6 − 360 147 y n + 5 + 450 147 y n + 4 − 400 147 y n + 3 + 225 147 y n + 2 − 72 147 y n + 1 + 10 147 y n = 60 147 h f ( t n + 6 , y n + 6 ) . {\displaystyle y_{n+6}-{\tfrac {360}{147}}y_{n+5}+{\tfrac {450}{147}}y_{n+4}-{\tfrac {400}{147}}y_{n+3}+{\tfrac {225}{147}}y_{n+2}-{\tfrac {72}{147}}y_{n+1}+{\tfrac {10}{147}}y_{n}={\tfrac {60}{147}}hf(t_{n+6},y_{n+6}).}

s>6の場合、BDF方法は零点安定性（英語版）が失われるため使えなくなる[3]。

安定性

硬い微分方程式の解を計算する数値解法の安定性は、複素数平面に絶対安定性（absolute stability；または線型安定性、linear stability）の保証できるエリアとして示されている。BDF方法の絶対安定性領域 (region of absolute stability) は下記プロットのピンクエリアである。

安定性領域が左複素数平面を含む数値解法はA-安定(A-stable)と呼ばれる。数値解法がA-安定のほうが一番理想的だが、線型多段法に限って3段以上の方法はA-安定ではないと証明できる。プロットから見ると、3段以上のBDFの安定性領域はほとんどの左複素数平面とすべての負の実軸を含んでいる。そのような広い安定性領域を持つ線型多段法の中では、BDFが一番効率的だと考えられる[4]。

ピンクの領域はBDF方法の安定性領域を示している
  • BDF1
    BDF1
  • BDF2
    BDF2
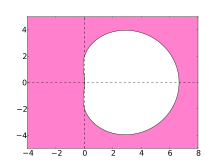  • BDF3
    BDF3
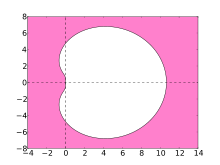  • BDF4
    BDF4
  • BDF5
    BDF5
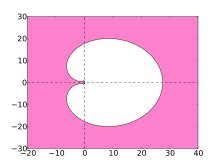  • BDF6
    BDF6

脚注

  1. ^ Ascher 1998, p. 129, §5.1.2
  2. ^ Iserles 1996, p. 27 (for s = 1, 2, 3); Süli & Mayers 2003, p. 349 (for all s)
  3. ^ Süli & Mayers 2003, p. 349
  4. ^ Süli & Mayers 2003, p. 349

参考文献

  • Ascher, U. M.; Petzold, L. R. (1998), Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, SIAM, Philadelphia, ISBN 0-89871-412-5 .
  • Iserles, Arieh (1996), A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press, ISBN 978-0-521-55655-2 .
  • Süli, Endre; Mayers, David (2003), An Introduction to Numerical Analysis, Cambridge University Press, ISBN 0-521-00794-1 .

外部リンク

  • BDF Methods at the SUNDIALS wiki (SUNDIALS is a library implementing BDF methods and similar algorithms).