Wet van Rayleigh-Jeans

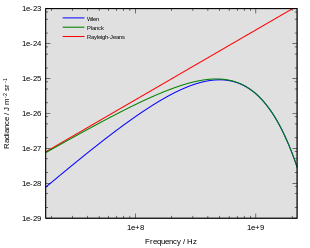
De wet van Rayleigh-Jeans is een voorloper op basis van de klassieke natuurkunde van de wet van Planck (voor de warmtestraling van een object), die voor grote waarden van het product van golflengte en absolute temperatuur een goede benadering daarvan is.

In 1900 stelden lord Rayleigh en sir Jeans de volgende redenering voor warmtestraling voor;

Stellen we ons een holle ruimte of caviteit voor met volume V waarvan de wanden een temperatuur T hebben, dan zenden deze wanden warmtestraling uit. In thermisch evenwicht heeft deze het spectrum van een zwart lichaam bij temperatuur T. Bij dit evenwicht bestaat deze warmtestraling uit staande golven (wegens interferentie) met knopen op de wanden. In dit systeem is de totale energie in de caviteit de som van de energieën van alle mogelijke staande golven.

De spectrale stralingsenergiedichtheid ${\displaystyle w_{\nu }}$ is dan

${\displaystyle w_{\nu }={\frac {N_{\nu }}{V}}\varepsilon }$

met ${\displaystyle N_{\nu }={\frac {8\pi \nu ^{2}}{c^{3}}}V}$ het aantal staande golven met frequentie ${\displaystyle \nu }$, ${\displaystyle V}$ het volume van de caviteit en ${\displaystyle \varepsilon =kT}$ de gemiddelde energie van de golven, ofwel:

${\displaystyle w_{\nu }={\frac {8\pi \nu ^{2}}{c^{3}}}kT}$

of gegeven als functie van de golflengte ${\displaystyle \lambda =c/\nu }$

${\displaystyle w_{\lambda }={\frac {8\pi }{\lambda ^{2}c}}kT}$

Deze wet komt enkel voor kleine frequenties goed overeen met het experiment. Voor grote frequenties gaat ${\displaystyle w_{\nu }\to \infty }$ terwijl experimenteel wordt gevonden dat ${\displaystyle w_{\nu }\to 0}$. Deze discrepantie staat bekend als de ultravioletcatastrofe.

In 1900 werd door Max Planck een aanpassing gemaakt:

${\displaystyle f(\lambda )={\frac {8\pi hc}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}}$