Cauchyfördelning

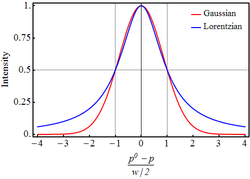
Cauchyfördelningen, även kallad Cauchy-Lorentzfördelningen, är en sannolikhetsfördelning inom matematisk statistik, uppkallad efter Augustin Louis Cauchy och Hendrik Lorentz. Den används bland annat för att beskriva vissa resonansfenomen inom fysiken.

Definition

Cauchyfördelningen kan definieras genom sin täthetsfunktion: ^[1]

${\displaystyle {\begin{aligned}f(x;x_{0},\gamma )&={\frac {1}{\pi \gamma \left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}\\[0.5em]&={1 \over \pi }\left[{\gamma \over (x-x_{0})^{2}+\gamma ^{2}}\right]\end{aligned}}}$

Här är ${\displaystyle x_{0}}$ medianvärdet, och ${\displaystyle \gamma }$ en skalningsparameter. När ${\displaystyle x_{0}=0,\gamma =1}$ fås en standardiserad Cauchyfördelning.

Egenskaper

Cauchyfördelningen är ett exempel på en sannolikhetsfördelning som saknar väntevärde, och därmed också varians.^[1] Detta beror på att integralen som beskriver väntevärdet blir odefinierad för Cauchyfördelningen, eftersom täthetsfunktionen inte avtar tillräckligt snabbt långt från origo. Med andra ord är Cauchyfördelningen ett exempel på en fördelning med "tunga svansar".

En standardiserad Cauchyfördelad stokastisk variabel kan även ses som en t-fördelad stokastisk variabel med en enda frihetsgrad.

Det gäller också att kvoten mellan två oberoende standardiserade normalfördelade stokastiska variabler är en standardiserad Cauchyfördelad stokastisk variabel.^[2]

Källor

Noter

Referenser

• Råde, Lennart; Bertil Westergren (1989). Mathematics Handbook for Science and Engineering (Beta). Lund: Studentlitteratur. ISBN 91-44-00839-2 

Externa länkar

• Wikimedia Commons har media som rör Cauchyfördelning.
  Bilder & media