Gömb

Ennek a szócikknek a megírásához egyetlen vagy kevés forrást használtak fel, ezért a szócikk tartalma egyoldalú is lehet. Az ellenőrizhetőség érdekében segíts a szócikk fejlesztésében további megbízható források hozzáadásával. (2023 januárjából)

Ez a szócikk a geometriai alakzatról szól. Hasonló címmel lásd még: A gömb (egyértelműsítő lap).

A gömb egy geometriai alakzat, mely jelenthet egy felületet (pontosabb megnevezése gömbhéj, esetleg üres gömb) és egy (tömör) testet egyaránt. A (héj)felület esetén egy adott ponttól a térben egyenlő távolságra lévő pontok, míg test esetén a legfeljebb az adott távolságra lévő pontok halmazát értjük rajta.

A gömböt tekinthetjük a kör általánosításának is.

Definíció

Gömbnek nevezzük a térben azon pontok halmazát, melyek egy adott P ponttól legfeljebb egy rögzített r távolságra vannak. Ekkor P-t a gömb középpontjának, r értékét pedig a gömb sugarának nevezzük. A P ponttól pontosan r távolságra lévő pontokat együttesen a gömb felületének, vagy felszínének nevezzük. Ha r = 1, akkor egységgömbről beszélünk.

Egyenletek

Az analitikus geometriában, az (x₀, y₀, z₀) középpontú és r sugarú gömböt azok az (x, y, z) pontok alkotják, melyekre fennáll az alábbi egyenlőtlenség:

${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}\leq r^{2}\,}$

Az egyenlőség a felületi pontokban teljesül:

${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=r^{2}\,}$

A belső pontokban szigorú egyenlőtlenség áll fenn:

${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}<r^{2}\,}$

Az r sugarú gömb felületi pontjai paraméterezhetőek a gömbi koordináták segítségével is:

${\displaystyle x=x_{0}+r\sin \theta \;\cos \phi }$

${\displaystyle y=y_{0}+r\sin \theta \;\sin \phi \qquad (0\leq \theta \leq \pi {\mbox{, }}-\pi <\phi \leq \pi )\,}$

${\displaystyle z=z_{0}+r\cos \theta \,}$

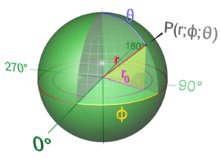
Az origó középpontú, tetszőleges sugarú gömbfelület a következő differenciálegyenlettel írható le:

${\displaystyle x\,dx+y\,dy+z\,dz=0.}$

Az egyenlet jól visszatükrözi a tényt, hogy a gömbfelületen mozgó pont helyvektora és sebességvektora mindig merőleges egymásra.

Vektortérben

Legyen ${\displaystyle V}$ egy (nem feltétlenül véges dimenziós) vektortér valamely ${\displaystyle \|.\|}$ normával. Ekkor a ${\displaystyle v\in V}$ középpontú ${\displaystyle r}$ sugarú gömbfelület megfogalmazható a következőképpen:

${\displaystyle G:=\{u\in V:\|u-v\|=r\}}$

Észrevehető, hogy háromdimenziós esetben a klasszikus gömbfelülethez, kétdimenzióban a körhöz jutunk az euklideszi normával.

A gömb belső pontjainak halmaza, más szóval a ${\displaystyle v\in V}$ pont ${\displaystyle r}$ sugarú környezete, szintén a háromdimenziós eset általánosításaként adható meg.

${\displaystyle K_{r}(v):=\{u\in V:\|u-v\|<r\}}$

Metrikus térben

Legyen ${\displaystyle (X,\rho )}$ metrikus tér. Ekkor a ${\displaystyle x\in X}$ középpontú ${\displaystyle r}$ sugarú gömbfelület megfogalmazható a következőképpen:

${\displaystyle G_{r}(x):=\{y\in X:\rho (x,y)=r\}}$

A gömb belső pontjai pedig egyenlőtlenség segítségével:

${\displaystyle K_{r}(x):=\{y\in X:\rho (x,y)<r\}}$

Utóbbit nevezik nílt gömbnek is, a ${\displaystyle G_{r}(x)\cap K_{r}(x)}$ halmazt pedig zárt gömbnek. Ezeknek lényeges analízisbeli alkalmazásaik vannak.

Forgástestként

A gömb úgy is definiálható, hogy az a test, ami egy kört átmérője körül megforgatva keletkezik. Ha a kört ellipszissel helyettesítjük, akkor az eredmény forgásellipszoid lesz.

Terminológia

Egy egyenes, ami metszi a gömböt, legfeljebb két pontban metszi. Ha a gömb egy pontpárján átmenő egyenes tartalmazza a gömb középpontját, akkor a pontpár egyik eleme a másik átellenes vagy antipodális pontja. Egy kör a gömb főköre, ha teljes egészében rajta van a gömbön, és középpontja megegyezik a gömb középpontjával.

Bár a Föld nem pontosan gömb, vagy forgásellipszoid alakú, gömbök esetén gyakran alkalmazzuk a Földre és más csillagászati testekre megszokott terminológiát. Ha egy gömbi pontot Északi-sarknak nevezünk, akkor átellenes pontja a Déli-sark, az egyenlítő pedig a pontpár két tagjától egyenlő távolságra húzódó főkör. A két sarkot összekötő körök a hosszúsági körök, vagy meridiánok. Az egyenlítővel párhuzamos körök a szélességi körök.

Felszín és térfogat

A gömb felszíne:

${\displaystyle A=4\pi r^{2}\,}$,

a térfogata pedig:

${\displaystyle V={\frac {4\pi r^{3}}{3}}}$.

Ezeket többféleképpen, integrálszámítással, közelítő poliéderekkel vagy a Cavalieri-elv segítségével lehet belátni.

A gömbnek van a legkisebb felülete az adott térfogatú testek közül. Másként fogalmazva, rögzített felület esetén a gömb rendelkezik a testek közül a legnagyobb térfogattal (izoperimetrikus egyenlőtlenség). Ennek folyománya, hogy a szabad folyadékfelszínek a gömbhöz minél inkább közeli alakzatokat igyekszenek felvenni.

Egy adott gömb körülírt hengerének térfogata éppen másfélszerese a gömb térfogatának, és a felszíne is másfélszerese a gömb felszínének. Ezt már Arkhimédész is tudta. Ennek belátásához írjuk fel a henger térfogatát és felszínét is:

${\displaystyle {\begin{aligned}A&=2\pi r^{2}+2\pi r\cdot 2r=6\pi r^{2}\\V&=\pi r^{2}\cdot 2r=2\pi r^{3}\end{aligned}}}$.

Elvégezve az osztásokat kapjuk az eredményt.^{[* 1]}

Gömbi geometria

A gömb felületének pontjai is alkalmasak geometria bevezetésére, ezt gömbi geometriának nevezzük. Ennek a geometriának főleg a távolsági közlekedésben van szerepe, de sok elméleti alkalmazása is van. Ugyanakkor jó néhány meglepő vagy váratlan tulajdonsággal is rendelkezik, ez pedig a szemlélet fejlesztésére is alkalmassá teszi. Az egyik legismertebb ilyen a navigációs paradoxon, ami szerint a "legrövidebb" és "legegyenesebb" útvonalak különböznek.

Például a Földön, mivel jó közelítéssel gömbnek tekinthető, egy objektum helyzetét megadhatjuk a Föld középpontjától való R távolsággal, a λ hosszúsági fokkal,^{[* 2]} és a φ szélességi fokkal.^{[* 3][1]} Sokszor a távolságot nem adják meg, mivel a felszínen közel állandó^{[* 4]}, legfeljebb amikor lényeges, a felszíntől mért távolság formájában. Ezen paramétereket földrajzi koordináta-rendszernek is nevezik. Ennek a leképezésnek egyik folyománya, hogy a gömb ekvivalens egy ${\displaystyle [0;R]\times [0;2\pi ]\times [0;\pi ]}$ kockával.

Topológia

Az n-gömb olyan topologikus tér, ami homeomorf az n+1 dimenziós golyó határával. Magyarul, homeomorf az euklideszi n-gömbbel.

• A 0-gömb pontpár a diszkrét topológiával
• Az 1-gömb homeomorf a körrel; tehát minden csomó 1-gömb
• A 2-gömb homeomorf a (közönséges) gömbbel. Így minden ellipszoid 2-gömb.

Az n-gömböt Sⁿ-nel jelölik. Ez kompakt topologikus sokaság, aminek nincs határa. Nem feltétlenül differenciálható; ha mégis, akkor lehet, hogy nem diffeomorf az euklideszi gömbbel.

Az euklideszi n-gömb kompaktsága könnyen bizonyítható a Borel–Lebesgue-tétellel:

A gömb egy egypontú halmaz ősképe az ||x|| folytonos függvényre nézve, ezért a gömb zárt. Sⁿ nyilván korlátos is. Tehát korlátos és zárt, így kompakt. Az n-dimenziós gömb térfogata ${\displaystyle r=1}$-re ${\displaystyle n=5}$-ig növekszik, majd a nullához konvergál.^[2]

További információk

• Mathworld honlap (angol)
• További gömbábrázolások a Vidám Matek angol honlapról
• Vetülettan (magyar)

Megjegyzések

Források