Gráfszorzás

A matematika, azon belül a gráfelmélet területén a gráfszorzás olyan kétváltozós gráfművelet, amely gráfok rendezett párjaihoz egy új gráfot rendel. Specifikusan: a két bemeneti gráf, G₁ és G₂ alapján kimenetként a következő tulajdonságokkal rendelkező H-t adja:

• H csúcshalmaza a V(G₁) × V(G₂) Descartes-szorzat, ahol V(G₁) és V(G₂) a G₁, illetve a G₂ csúcshalmazai.
• Két H-beli csúcs (u₁, u₂) és (v₁, v₂) pontosan akkor szomszédosak, ha az u₁, u₂, v₁, v₂ csúcsokra teljesül valamely G₁ és G₂ éleire vonatkozó feltétel. A gráfszorzatok különböző fajtái éppen ebben a feltételben térnek el.

A különböző gráfszorzatok leírása és jelölése az irodalomban erősen változó lehet; bár az alább alkalmazott jelölések elég elterjedtek, érdemes egy-egy cikk olvasásakor ellenőrizni, hogy az adott szerző egy gráfszorzat mely definícióját használja, főleg régebbi szövegekben.

Áttekintő táblázat

A következő táblázat felsorolja az elterjedtebb gráfszorzatokat. A ${\displaystyle \sim }$; jelentése „a két csúcs össze van kötve”, míg a ${\displaystyle \not \sim }$ az össze nem kötöttséget jelöli. A táblázatban alkalmazott szimbólumok nem tekinthetők univerzálisan elfogadottnak, különösen a régi cikkekben találhatók egyedi jelölések.

Név	${\displaystyle (u_{1},u_{2})\sim (v_{1},v_{2})}$ feltétele	Méret (élek száma) ${\displaystyle {\begin{array}{cc}n_{1}=\vert \mathrm {V} (G)\vert &n_{2}=\vert \mathrm {V} (H)\vert \\m_{1}=\vert \mathrm {E} (G)\vert &m_{2}=\vert \mathrm {E} (H)\vert \end{array}}}$	Példa
Descartes-szorzat 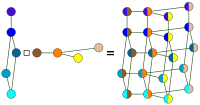${\displaystyle G\square H}$	( ${\displaystyle u_{1}}$ = ${\displaystyle v_{1}}$ és ${\displaystyle u_{2}}$ ${\displaystyle \sim }$ ${\displaystyle v_{2}}$ ) vagy ( ${\displaystyle u_{1}}$ ${\displaystyle \sim }$ ${\displaystyle v_{1}}$ és ${\displaystyle u_{2}}$ = ${\displaystyle v_{2}}$ )	${\displaystyle m_{2}n_{1}+m_{1}n_{2}}$
Tenzorszorzat (kategóriaszorzat) ${\displaystyle G\times H}$	${\displaystyle u_{1}}$ ${\displaystyle \sim }$ ${\displaystyle v_{1}}$ és  ${\displaystyle u_{2}}$ ${\displaystyle \sim }$ ${\displaystyle v_{2}}$	${\displaystyle 2m_{1}m_{2}}$
Lexikografikus szorzat ${\displaystyle G\cdot H}$ vagy ${\displaystyle G[H]}$	u1 ∼ v1 vagy ( u1 = v1 és u2 ∼ v2 )	${\displaystyle m_{2}n_{1}+m_{1}n_{2}^{2}}$
Erős szorzat (Normál szorzat, ÉS szorzat) ${\displaystyle G\boxtimes H}$	( u1 = v1 és u2 ∼ v2 ) vagy ( u1 ∼ v1 és u2 = v2 ) vagy ( u1 ∼ v1 és u2 ∼ v2 )	${\displaystyle n_{1}m_{2}+n_{2}m_{1}+2m_{1}m_{2}}$
Ko-normális szorzat (diszjunktív szorzat, VAGY szorzat) ${\displaystyle G*H}$	u1 ∼ v1 vagy u2 ∼ v2
Moduláris szorzat	${\displaystyle (u_{1}\sim v_{1}}$ és ${\displaystyle u_{2}\sim v_{2})}$ vagy ${\displaystyle (u_{1}\not \sim v_{1}}$ és ${\displaystyle u_{2}\not \sim v_{2})}$
Gyökeres szorzat	Lásd a szócikket	${\displaystyle m_{2}n_{1}+m_{1}}$
Cikkcakkszorzat	Lásd a szócikket	Lásd a szócikket	Lásd a szócikket
Replacement szorzat
Homomorf szorzat[1][3] ${\displaystyle G\ltimes H}$	${\displaystyle (u_{1}=v_{1})}$ vagy ${\displaystyle (u_{1}\sim v_{1}}$ és ${\displaystyle u_{2}\not \sim v_{2})}$

Általában egy gráfszorzat értékét az (u₁, u₂) ∼ (v₁, v₂)-re vonatkozó olyan feltétel határozza meg, ami a következő kifejezések segítségével megadható: u₁ ∼ v₁, u₂ ∼ v₂, u₁ = v₁ vagy u₂ = v₂.

Mnemonik

Néhány egyszerű trükk segít megkülönböztetni a sokféle gráfszorzatot.

Jelöljük a két csúcsú teljes gráfot (ami egyetlen élből áll) ${\displaystyle K_{2}}$-vel. Ekkor a ${\displaystyle K_{2}\square K_{2}}$, ${\displaystyle K_{2}\times K_{2}}$ és ${\displaystyle K_{2}\boxtimes K_{2}}$ szorzatgráfok éppen úgy néznek ki, mint az őket előállító műveleti jel. Például a ${\displaystyle K_{2}\square K_{2}}$ a négy csúcsból álló kör (négyzet) és ${\displaystyle K_{2}\boxtimes K_{2}}$ a négy csúcsú teljes gráf. A lexikografikus szorzás jelölése – ${\displaystyle G[H]}$ – arra emlékeztet, hogy ez a szorzástípus nem kommutatív.

Kapcsolódó szócikkek

• Gráfművelet

Jegyzetek