Rezgés

A mechanikai rezgés vagy lengés oszcilláló mozgást jelent egy egyensúlyi állapot körül. Az oszcillálás lehet periodikus, mint például egy inga esetén, vagy rendezetlen, véletlenszerű, mint például egy gépkocsikerék mozgása a karosszériához képest, göröngyös úton. A rezgés és lengés szavak fizikai tartalma azonos, a magyar köznyelvben a gyors lengéseket rezgésnek szokás mondani, a lassúak a lengések. A testek rezgésével foglalkozó tudomány a lengéstan, de analízisével a rezgésanalízis foglalkozik.

A rezgés esetenként kívánatos lehet. Ilyen például a hangvilla, vagy a nyelvsíp rezgése fúvós hangszerek vagy harmonika esetén, vagy egy hangszóró kúpjának rezgése, ezeknek az eszközöknek működéséhez elengedhetetlen a rezgésük.

Sok esetben a rezgés kerülendő, mivel energiaveszteséget, nemkívánatos hangot, zajt okoz, kopással jár és instabilitáshoz, akár anyagtöréshez is vezethet. Így például gépek, motorok, vagy bármely mechanikus eszköz működésekor általában károsak a rezgések. A rezgéseket okozhatja a forgórészek kiegyensúlyozatlansága, súrlódás, rosszul illeszkedő, kopott fogaskerekek, stb. A gondos tervezés és kivitelezés a nemkívánatos rezgéseket általában minimálisra csökkenti.

A hangok, a zaj és a rezgés vizsgálata szorosan összefüggő területek. A hangot, vagyis a nyomáshullámokat rezgő szerkezetek keltik (például a hangszálak) és nyomáshullámok rezgéseket tudnak kelteni (például a dobhártyán). Ilyen módon, ha zajcsökkentésre törekszünk, az gyakran rezgéscsökkentéssel érhető el.

Rezgéstípusok

Szabad rezgés akkor alakul ki, ha egy mechanikai rendszert kezdeti állapotba „húzunk fel”, majd engedjük, hogy szabadon rezegjen. Ennek példája lehet az, ha egy gyereket meglendítünk a hintán, majd magára hagyjuk, vagy megütünk egy hangvillát és hagyjuk zengeni. A mechanikai rendszer ekkor rezgéseket fog végezni egy vagy több sajátfrekvenciájával, majd a rezgés csillapodik és megáll.

Gerjesztett rezgés során a mechanikai rendszerre alternáló erő vagy mozgás hat. Példa erre egy rosszul kiegyensúlyozott mosógép rázkódása, a közlekedés okozta rezgés (melyet elhaladó teherautó okoz) vagy egy épület rezgése földrengés folyamán.

A gerjesztett rezgés során a rezgés frekvenciája a gerjesztés frekvenciájától függ, de erőssége szoros összefüggésben van a mechanikai rendszer jellemzőivel.

Rezgésvizsgálat

A rezgésvizsgálat alapjait egy egyszerű tömeg-rugó modell, úgynevezett egytömegű lengőrendszer viselkedésén lehet megérteni. Valóban, egy olyan összetett szerkezet viselkedését, mint amilyen egy gépkocsi, részenkénti tömeg-rugó-csillapítás modellek összerakásával lehet modellezni. A tömeg-rugó-csillapítás modell az egyszerű harmonikus oszcillátor példája, és így a viselkedését leíró matematikai eszközök azonosak más egyszerű harmonikus oszcillátorok vizsgálatával, mint amilyen például egy egyszerű villamos rezgőkör.

Megjegyzés: Ez a szócikk nem tartalmazza a lépésenkénti matematikai levezetést, csak a fontosabb egyenleteket és a rezgésvizsgálat fontosabb elveit mutatjuk meg. Amennyiben az olvasót a részletek érdeklik, forduljon a hivatkozott irodalomhoz.

Csillapítatlan szabad rezgés

Egyszerűsége miatt vizsgáljuk meg a tömeg–rugó rendszert abban az esetben, ha minden csillapítást elhanyagolunk és nincs külső erő, amely hatna a rendszerre (vagyis a rendszer szabad rezgést végez).

A tömegre ható rugóerő arányos az „x” kitéréssel (feltételezzük, hogy nyugalmi állapotban a rugót a tömeg súlya már előfeszítette). Az arányossági együttható, k a rugómerevség, egysége erő/elmozdulás (N/m):

${\displaystyle F_{s}=-kx\!}$

A tömegre ható tehetetlenségi erő Newton 2. törvénye szerint arányos a gyorsulással:

${\displaystyle \Sigma \ F=ma=m{\ddot {x}}=m{\frac {d^{2}x}{dt^{2}}}}$

A tömegre ható erők összege az alábbi közönséges differenciálegyenletre vezet:

${\displaystyle m{\ddot {x}}+kx=0.}$

Ha feltesszük, hogy a rezgés kezdetekor a rugót “A” értékkel megnyújtjuk, majd elengedjük, a mozgásegyenlet a következő alakú lesz:

${\displaystyle x(t)=A\ cos(\omega _{k}t)=A\cos(2\pi f_{k}t)=A\sin {\frac {2\pi }{T}}t\!}$, ahol T a periódusidő.

A megoldás azt mondja, hogy a rendszer “A” amplitúdójú és ${\displaystyle f_{n}}$ frekvenciájú egyszerű harmonikus rezgőmozgást fog végezni. De mi is az ${\displaystyle f_{k}}$? ${\displaystyle f_{k}}$ a rezgésanalízis egyik legfontosabb mennyisége, melyet csillapítatlan sajátfrekvenciának hívnak. Az ${\displaystyle f_{k}}$ egytömegű lengőrendszer esetén:

${\displaystyle f_{k}={1 \over {2\pi }}{\sqrt {k \over m}}\!,}$

illetve az ennek megfelelő szögsebesség:

${\displaystyle \omega _{k}={\sqrt {k \over m}}\!.}$

Megjegyzés: Az ${\displaystyle \omega }$ szögsebességet, (${\displaystyle \omega =2\pi f}$) radián/s egységgel gyakran használják az összefüggésekben, mert egyszerűvé teszi a kifejezéseket, a frekvencia mértékegysége a Hz, vagy azzal egyenlő rezgés/másodperc).

Ha ismerjük a rendszer tömegét és rugómerevségét, a fenti képlettel kiszámíthatjuk azt a frekvenciát, mellyel a rendszer rezegni fog, ha a nyugalmi helyzetéből egy kezdeti zavarás kitéríti, majd magára hagyjuk. Minden lengőrendszernek egy vagy több sajátfrekvenciája van, mellyel a szabad lengéseit (rezgéseit) végzi. Ennek az egyszerű összefüggésnek segítségével megmagyarázható, mi történik egy összetett rendszerrel, ha további tömeget vagy rugót adunk hozzá.

Például, ha egy teherautót teljesen megrakodnak, a rugózása érezhetően “lágyabb” lesz az üres kocsiéhoz képest, mivel a tömegét megnöveltük és így a sajátfrekvenciája csökken.

Mi okozza a rendszer rezgését, ha nem hat rá gerjesztőerő?

Ezek a képletek leírják a mozgást, de nem magyarázzák meg, miért mozog a rendszer. A rendszer mozgása az energia megmaradásával magyarázható. A fenti példában “A” értékkel megnyújtottuk a rúgót és így ${\displaystyle {\tfrac {1}{2}}kA^{2}}$ potenciális energiát tároltunk a rugóban.

Ha elengedjük a rugót, a rugó igyekszik visszatérni terheletlen állapotába és ennek folyamán felgyorsítja a tömeget. Azon a ponton, ahol a rugó eléri terheletlen állapotát, nem tárol többé energiát, de a tömeg elért legnagyobb sebességét és így minden energia átalakult ${\displaystyle {\tfrac {1}{2}}mv^{2}}$ mozgási energiává. Ettől kezdve a tömeg mozgása lassulni fog, mert így a másik irányba nyomja össze a rugót és a mozgási energia fokozatosan átalakul ismét potenciális energiává. Az energiának ez az átalakulása kinetikus energiából potenciális energiává és vissza okozza a tömeg oszcilláló mozgását.

A fenti egyszerű modellben a tömeg a rezgést örökké folytatni fogja a kezdeti amplitúdóval, de a valóságos rendszerekre mindig hat valamiféle csillapítás, mely az energiát elnyeli és így a rendszer rezgése előbb-utóbb megszűnik.

Csillapított szabad rezgés

Az előbbi modellt most egészítsük ki viszkózus csillapítással, melyet az jellemez, hogy a csillapító erő arányos a tömeg sebességével. Ezt a csillapítást viszkózusnak nevezik, mivel a folyadék csillapítását modellezi. A “c” arányossági tényezőt csillapítási tényezőnek nevezik, mértékegysége N s/m.

${\displaystyle F_{c}s=-cv=-c{\dot {x}}=-c{\frac {dx}{dt}}\!}$

Összegezve a tömegre ható erőket az alábbi közönséges differenciálegyenletet kapjuk:

${\displaystyle m{\ddot {x}}+{c}{\dot {x}}+{k}x=0.}$

Az egyenlet megoldása a csillapítás mértékétől függ. Ha a csillapítás eléggé kicsi, a rendszer rezegni fog, de idővel megszűnik a rezgése. Ez az eset a gyakorlat szempontjából a legfontosabb. Ha a csillapítást addig növeljük, míg a rendszer éppen megszűnik rezegni, akkor elértük a kritikus csillapítást. A kritikus csillapításhoz tartozó csillapítási tényező értéke egytömegű lengőrendszer esetén:

${\displaystyle c_{k}=2{\sqrt {km}}}$

A rendszer csillapításának mértékéül a csillapítási viszonyt vezették be. (Ezt csillapítási faktornak vagy a kritikus csillapítás %-ának is hívják). Ez a csillapítási viszony a tényleges csillapítási tényező és a kritikus csillapítási tényező hányadosa. Képlete az egytömegű lengőrendszer esetén:

${\displaystyle \zeta ={c \over 2{\sqrt {km}}}.}$

A fémszerkezetek (például egy repülőgép törzs, belsőégésű motor forgattyús tengelye) csillapítási viszonya 0,05-nél kevesebb, gépkocsi kerékfelfüggesztése esetén 0,2-0,3 között van.

A csillapított modell differenciálegyenletének megoldása:

${\displaystyle x(t)=Xe^{-\zeta \omega _{k}t}\cos({{\sqrt {1-\zeta ^{2}}}\omega _{k}t-\phi }),\ \ \omega _{k}=2\pi f_{k}}$

“X” értéke a kitérés kezdeti értéke és ${\displaystyle \phi }$ a fázisszög. Ezeknek az értékeknek a képlete a referenciákban található.

A képletben két dolgot kell kiemelni. Az egyik az exponenciális kifejezés, amely azt mutatja, hogy a rezgés milyen gyorsan csillapodik le – minél nagyobb a csillapítási viszony, annál gyorsabban tart a kitérés nullához. A másik a koszinuszfüggvény, ez az eredmény oszcilláló része, de a rezgés frekvenciája eltér a csillapítás nélküli esetétől.

Az ${\displaystyle f_{cs}}$ sajátfrekvenciát ebben az esetben csillapított sajátfrekvenciának nevezik, összefüggése a csillapítatlan sajátfrekvenciával az alábbi:

${\displaystyle f_{cs}={\sqrt {1-\zeta ^{2}}}f_{k}}$

A csillapított sajátfrekvencia kisebb, mint a csillapítatlan, de sok gyakorlati esetben a csillapítási viszony kicsi és így a különbség elhanyagolható. Ezért a csillapított és csillapítatlan jelzőt gyakran elhagyják a sajátfrekvencia elől (például 0,1 csillapítási viszonynál a csillapított sajátfrekvencia csak 1%-kal kisebb, mint a csillapítatlan).

A jobb oldali diagramok azt mutatják, hogy 0,1 és 0,3 csillapítási viszony esetén hogy cseng le a rezgés. A gyakorlatban gyakran úgy mérik a csillapítást, hogy egy ütés (például kalapácsütés) után kísérletileg meghatározzák a sajátfrekvenciát a lengések gyakoriságából és a csillapítási viszonyt a kitérések csökkenésének mértékéből. A sajátfrekvencia és a csillapítási viszony ismerete nemcsak a szabadlengések esetén fontos, hanem meghatározza a rendszer viselkedését a gerjesztett rezgések esetén is.

Gerjesztett rezgés csillapítással

Ebben a fejezetben az egytömegű, csillapított lengőrendszer viselkedését vizsgáljuk az alábbi harmonikus gerjesztőerő hatására. Ilyen gerjesztést például forgó, kiegyensúlyozatlan tömeg kelt.

${\displaystyle F=F_{0}\cos {(2\pi ft)}\!}$

Ha ismét összegezzük a lengőrendszer tömegére ható erőket, az alábbi közönséges differenciálegyenletet kapjuk:

${\displaystyle m{\ddot {x}}+{c}{\dot {x}}+{k}x=F_{0}\cos {(2\pi ft)}}$

Ennek az állandósult állapothoz tartozó megoldása:

${\displaystyle x(t)=X\cos {(2\pi ft-\varphi )}\!}$

Az eredmény szerint a tömeg a gerjesztés f frekvenciájával fog rezegni, de ${\displaystyle \phi }$ fáziskéséssel.

A rezgés “X” amplitúdóját az alábbi képlet határozza meg:

${\displaystyle X={F_{0} \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}}}$

Ahol “r” a harmonikus gerjesztés frekvenciájának és a csillapítás nélküli egytömegű lengőrendszer sajátfrekvenciájának hányadosa:

${\displaystyle r={\frac {f}{f_{n}}}}$

A ${\displaystyle \varphi }$ fáziskésés pedig:

${\displaystyle \varphi =\mathrm {arctg} {\left({\frac {2\zeta r}{1-r^{2}}}\right)}}$

Ezeknek a függvényeknek a grafikonjai, melyeket a rendszer gerjesztésre adott válaszának neveznek, a gerjesztett rezgés legfontosabb jellemzőit tartalmazzák. Gyengén csillapított rendszernél, ahol a gerjesztés frekvenciája a sajátfrekvenciához közel esik, igen nagy rezgésamplitúdó léphet fel. Ezt a jelenséget rezonanciának nevezik (emiatt a rendszer sajátfrekvenciáját gyakran rezonancia-frekvenciának is hívják).

A mechanikai rendszerekben fellépő rezonancia igen káros lehet – esetleg a rendszer meghibásodásához is vezethet. Ennélfogva a rezgésanalízis egyik fő oka az, hogy meghatározzuk, hol léphet fel rezonancia, és milyen rendszabályokat kell tenni, hogy elkerüljük fellépését. Az amplitúdó diagramja jól mutatja, hogy a rendszer csillapítását növelve érezhetően csökkenthető a rezgés erőssége. Hasonlóképpen a rezgéserősség csökkenthető, ha a sajátfrekvenciát eléggé messze visszük a gerjesztés frekvenciájától megváltoztatva a rendszer merevségét vagy tömegét. Ezt a műveletet nevezik elhangolásnak. Ha a rendszert nem lehet megváltoztatni, esetleg a gerjesztés frekvenciáján lehet változtatni (például megváltoztatni a gerjesztést létrehozó gép fordulatszámát).

Az alábbiakban a gerjesztésre adott frekvencia-válasz néhány további szempontját mutatjuk be.

• Adott frekvencia viszonynál az X rezgésamplitúdó egyenesen arányos az ${\displaystyle F_{0}}$ gerjesztőerő-amplitúdóval (vagyis például kétszer nagyobb erőre kétszer erősebb rezgés a válasz).
• Csillapítás nélküli vagy kis csillapítású esetben a rezgés és a gerjesztőerő fázisban van, ha r < 1 és 180º-ot késik, ha a frekvenciaviszony r > 1-nél.
• Ha r<<1, az amplitúdó megegyezik a rugó kitérésével ${\displaystyle F_{0}}$ statikus erő hatására. Így r<<1 esetén a tömeg és csillapítás hatása minimális.

• Ha r>>1, a rezgésamplitúdó kisebb, mint a rugó statikus erő hatására bekövetkező ${\displaystyle \delta _{st}}$ kitérése. Ebben a tartományban a tömeg által keltett F=ma erő hatása érvényesül, mert a gyorsulás növekszik a frekvenciával. Mivel az X rugókitérés csökken ebben a tartományban, az F=kx rugóerő is csökken. Ezért a tömeg-rugó-csillapítás rendszer alapja a harmonikus gerjesztőerőtől szigetelt lesz, ezért az ilyen rendszert rezgésszigetelésnek hívják. Érdekességképpen megemlítjük, hogy a csillapítás növelése rontja a rezgésszigetelés hatásosságát, ha r>>1, mivel az F=cv csillapító erő is átadódik az alapnak.

Mi okozza a rezonanciát?

A rezonanciát egyszerű megérteni, ha a tömeget kinetikusenergia-tárolónak, a rugót potenciálisenergia-tárolónak fogjuk fel. Ahogy korábban láttuk, ha sem a tömegre sem a rugóra nem hat külső erő, akkor a két energiafajtát folytonosan átalakítják egymásba a sajátfrekvencia gyakoriságával. Más szóval, ha hatékonyan közlünk energiát a tömeggel vagy a rúgóval, akkor a szabadlengések ütemében kell betáplálni az energiát. A tömeggel és a rugóval energiát közölni hasonló művelet, mint ahogy egy gyereket lökünk a hintán, a megfelelő pillanatban kell meglökni a hintát ahhoz, hogy egyre magasabbra repüljön. Ugyanúgy, mint a hinta esetében, az alkalmazott erőnek nem kell nagynak lennie ahhoz, hogy heves mozgást érjünk el. Csak arról kell gondoskodni, hogy az energiaátadás a megfelelő időben következzék be.

A csillapítás energiatárolás helyett felemészti az energiát. Mivel a csillapítóerő arányos a sebességgel, minél kisebb a kitérés (középső holtpontban a sebesség maximális, a gyorsulás nulla), annál több energiát nyel el a csillapítás. Ezért be fog következni egy ponton az, hogy a gerjesztő erő által betáplált energia és a csillapítás által elnyelt energia egyenlő lesz. Ennél az állapotnál a rendszer rezgési amplitúdója legnagyobb értékét éri el, és ezzel az amplitúdóval fog rezegni, amíg a gerjesztés változatlan marad. Ha nincs csillapítás, nincs ami elnyelje az energiát, és ezért elvileg a kitérés végtelenig fokozódik.

Összetett gerjesztés hatása az egytömegű lengőrendszerre

Eddig csak egy egyszerű harmonikus erőt vettünk figyelembe, de ez modell kiterjeszthető a több gerjesztő erő esetére is két fontos matematikai eszköz segítségével.

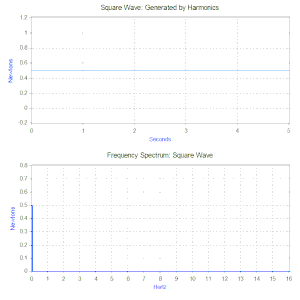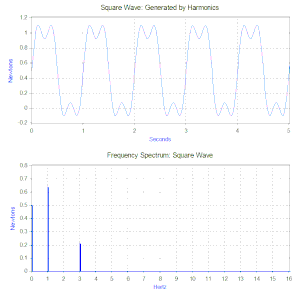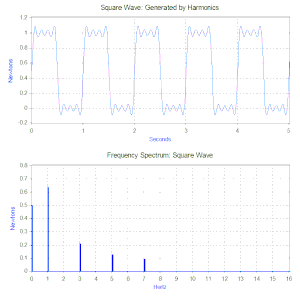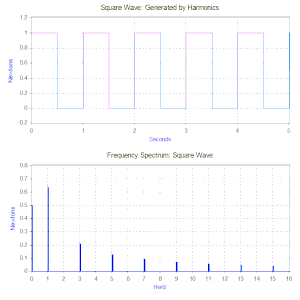
Az első a Fourier-transzformáció, mely az idő függvényében adott jelet harmonikus összetevőire bontja, így a frekvencia függvényébe képezi le. Például hasson egy tömeg-rugó-csillapítás modellre a következő ismétlődő gerjesztőerő ciklus: egy 1 newton nagyságú állandó erő 0,5 másodperig, majd 0,5 másodpercig ne hasson rá semmilyen erő. Az ilyen típusú gerjesztést 1 Hz-es négyszöghullámnak hívják.

A négyszöghullám Fourier-transzformáltja egy frekvencia spektrum lesz, vagyis sok egyszerű, de különböző frekvenciájú és amplitúdójú harmonikus rezgés összege, melyekből a négyszöghullám felépül. (A fázisszögek szintén meghatározhatók, de ezek kisebb jelentőségűek, legtöbbször nincs rájuk szükség.)

A Fourier-transzformáció nem periodikus függvények (impulzusok, véletlenszerű függvények) analizálására is alkalmas. A számítógépek a gyors Fourier-transzformáció (FFT) ablakfüggvényes változatával végzik ezeket a számításokat.

A példabeli négyszöghullám esetében (lásd az ábrát) az első komponens egy állandó 0,5 newton nagyságú erő, melyet a 0 Hz-hez tartozó érték képvisel a frekvenciaspektrumban. A következő komponens az 1 Hz frekvenciájú 0,64 amplitúdójú szinuszhullám. Ezt az ábrán az 1 Hz-nél felrajzolt függőleges egyenes jeleníti meg. A további komponensek a páratlan számú frekvenciákon látható végtelen sok szinuszhullámból állnak, melyek összességükben kiadják a négyszöghullámot. Ilyen módon a Fourier-transzformáció segítségével lehetővé válik a bonyolult alakú erőket harmonikus komponenseire bontani. Bár tetszőleges gerjesztés esetén (így a négyszöghullám esetén is) a Fourier-transzformáció végtelen sok harmonikus komponenst eredményez, gyakorlati vizsgálatokhoz (ahogy az ábrából is látható) az első néhány összetevő figyelembevétele elegendő, mert a magasabb frekvenciájú összetevők amplitúdója egyre kisebb.

Az előzőekben a gerjesztett rezgés időfüggvénye egyetlen harmonikus lefutású erőre lett megadva, de a Fourier-transzformáció általában több harmonikus erőt eredményez. Ha a rendszer lineáris, az egymástól függetlenül kiszámolt részmegoldásokat összegezni lehet a szuperpozíció elve értelmében. A tömeg-rugó-csillapítás modell esetén a rendszer lineáris, ha a rugóerő arányos a kitérítéssel és a csillapító erő arányos a tömeg mindenkori sebességével az egész működési tartományban. Így a rendszer válasza a négyszöghullám alakú gerjesztésre a harmonikus komponensekre adott válasz összegeként meghatározható.

Frekvencia válasz modell

Ebben a modellben a megoldást a bemenet (gerjesztés) és a kimenet (rezgésamplitúdó) egymáshoz való viszonyában keressük. Ha a gerjesztőerőt és a rezgéserősséget az ${\displaystyle \omega \,}$ frekvencia függvényének tekintjük, akkor felírhatjuk a következő egyenletet:

${\displaystyle X(\omega )=H(\omega )*F(\omega )\ \ vagy\ \ H(\omega )={X(\omega ) \over F(\omega )}}$

A ${\displaystyle H(\omega )\,}$ függvényt frekvencia válasz függvénynek vagy frekvencia átviteli függvénynek nevezik (ez utóbbi pontatlanabb elnevezés) és ha komplex számként definiáljuk, melynek valós és képzetes része is van, akkor nemcsak a rezgésamplitúdót, hanem a fázisszöget is tartalmazza. A frekvencia válaszfüggvény egytömegű csillapított lengőrendszerre már a korábbiakban bemutatásra került:

${\displaystyle |H(\omega )|=\left|{X(\omega ) \over F(\omega )}\right|={1 \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}}}$

ahol:

${\displaystyle r={\frac {f}{f_{n}}}={\frac {\omega }{\omega _{n}}}}$

A fázisszög a korábbiak ismeretében:

${\displaystyle \varphi =\angle H(\omega )=\mathrm {arctg} {\left({\frac {2\zeta r}{1-r^{2}}}\right)}}$

Például számítsuk ki egy 1 kg tömegből, 1,93 N/mm rugómerevségű rugóból és 0,1 csillapítású rendszernek a frekvencia válaszát. A csillapítás nélküli rendszer sajátfrekvenciája erre az esetre 7 Hz. Ha az előbbiekben vizsgált 1 Hz-es frekvenciájú négyszöghullámú gerjesztést alkalmazzuk a rendszerre, kiszámíthatjuk a frekvenciaválaszt. Az ábrán látható az eredményezett rezgés frekvenciaspektruma. A példa esetében a négyszöghullám negyedik harmonikusa 7 Hz-re esik. Az egytömegű lengőrendszer válasza 7 Hz-en tehát viszonylag nagy amplitúdót eredményez annak ellenére, hogy a gerjesztőerő 7 Hz-es harmonikus komponense viszonylag alacsony értékű. A példa azt mutatja, hogy az eredményezett rezgés erőssége mind a gerjesztés erősségétől, mind a rendszer tulajdonságaitól függ.

A frekvencia válasz függvényt nemcsak a rendszer tömeg-, merevségi és csillapítási viszonyainak ismeretével lehet kiszámítani, hanem méréssel is meg lehet határozni. Például, ha ismert amplitúdójú, de változó frekvenciájú harmonikus erővel gerjesztjük a rendszert, mérni lehet a rendszer válaszrezgéseit és így megismerhetők a rendszer rezgéstani jellemzői.

Irodalom

• Rao, Singiresu, Mechanical Vibrations, Addison Wesley, 1990, ISBN 0-201-50156-2
• Thompson, W.T., Theory of Vibrations, Nelson Thornes Ltd, 1996, ISBN 0-412-783908
• Hartog, Den, Mechanical Vibrations, Dover Publications, 1985, ISBN 0-486-647854
• Természettudományi Kislexikon. Akadémiai Kiadó, Budapest, 1971. ISBN 963-05-0893-1
• Feynman: Mai fizika. 2. kötet. Relativisztikus fizika. Forgó- és rezgőmozgás. Műszaki Könyvkiadó, Budapest, 1968.

Kapcsolódó szócikkek

• Gyorsulásmérő

További információk

• Fizikakönyv.hu – Mechanikai rezgések